HOW TO FIND THE INVERSE OF A GRAPH WITHOUT AN EQUATION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Copy the graphs of the following functions and in each case include the graphs of y = x and y = f -1(x):
Problem 1 :
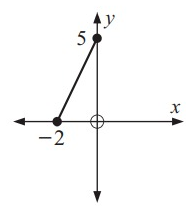
Solution:
Original function is a straight line. So, its inverse graph will also be a straight line.
Step 1 :
Mark some points from the original graph.
Step 2 :
Exchange the value of x and y. For example, (2, 5) will be converted as (5, 2).
Points from the graph :
(0, 5) ==> (5, 0)
(-2, 0) ==> (0, -2)
Step 3 :
Repeat this for all the point that we have taken from the original graph.
Step 4 :
Joint the point and draw the curve.
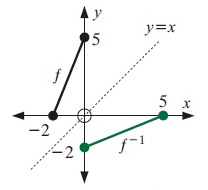
Problem 2 :
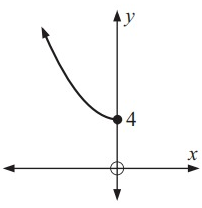
Solution :
Step 1 :
Mark some points from the original graph.
Step 2 :
Exchange the value of x and y.
Points from the graph :
(0, 4) ==> (4, 0)
Step 3 :
Repeat this for all the point that we have taken from the original graph.
Step 4 :
Joint the point and draw the curve.
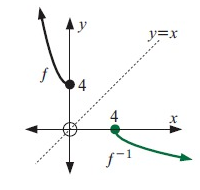
Problem 3 :
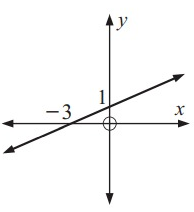
Solution:
Original function is a straight line. So, its inverse graph will also be a straight line.
Step 1 :
Mark some points from the original graph.
Step 2 :
Exchange the value of x and y.
Points from the graph :
(0, 1) ==> (1, 0)
(-.3, 0) ==> (0, -3)
Step 3 :
Repeat this for all the point that we have taken from the original graph.
Step 4 :
Joint the point and draw the curve.
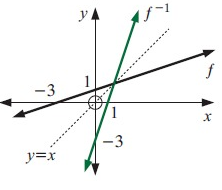
Problem 4 :
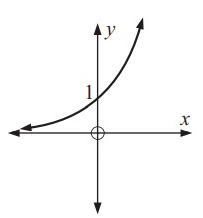
Solution:
Original function is a exponential graph. So, its inverse also be a exponential graph.
Step 1 :
Mark some points from the original graph.
Step 2 :
Exchange the value of x and y.
Points from the graph :
(0, 1) ==> (1, 0)
Step 3 :
Repeat this for all the point that we have taken from the original graph.
Step 4 :
Joint the point and draw the curve.
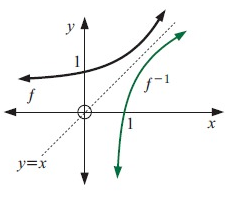
Problem 5 :
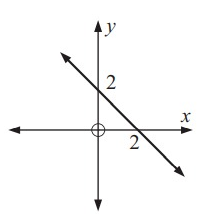
Solution:
Original function is a straight line. So, its inverse also be a straight line.
(2, 0) ==> (0, 2)
(0, 2) ==> (2, 0)
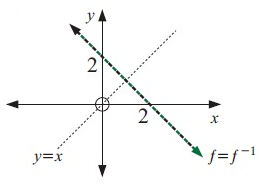
Problem 6 :
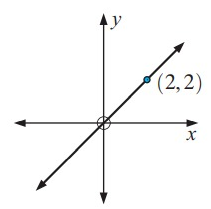
Solution:
Original function is a straight line. So, its inverse also be a straight line.
In this graph, point (2, 2) will be converted as (2, 2).
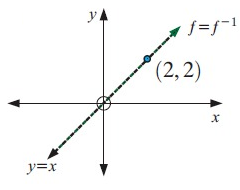
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling