GRAPHING ABSOLUTE VALUE FUNCTION AND FIND DOMAIN AND RANGE

Graph the following absolute value function. State the domain and range.

Problem 1 :

f(x) = |x| - 7

Solution :

Comparing with y = a|x - h| + k

The minimum point or vertex is at (0, -7). Since a is positive the absolute value function opens up.

Slope = 1

(-2, -5)(-1, -6) (0, -7) (1, -6) and (2, -5)

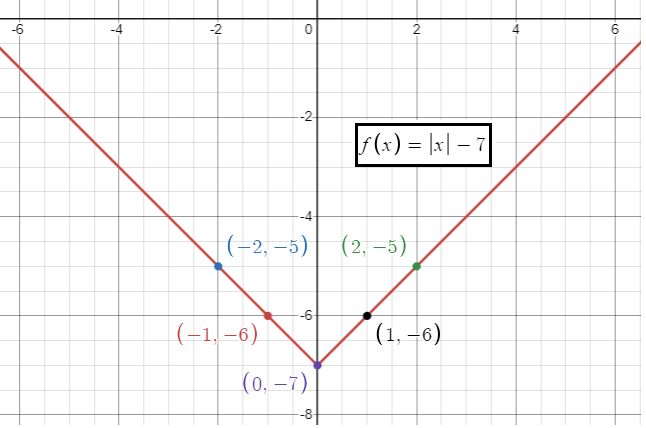
• Domain is all real values, that is  (-∞, ∞)
• Range is [-7, ∞)

Problem 2 :

f(x) = |x - 3| + 4

Solution :

Comparing with y = a|x - h| + k

The minimum point or vertex is at (3, 4). Since a is positive the absolute value function opens up.

Slope = 1

Some of the points on the absolute value function are (1, 6)(2, 5) (3, 4) (4, 5) and (5, 6)

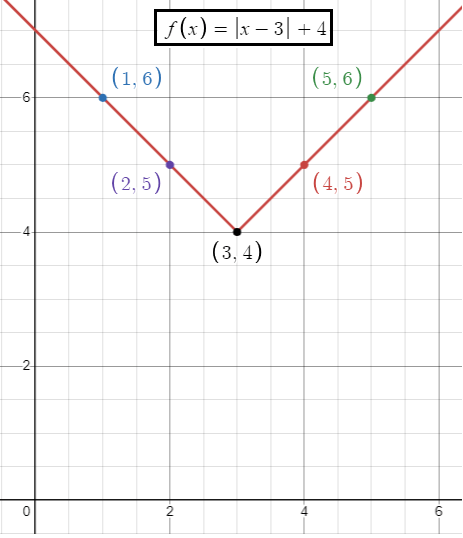
• Domain is all real values, that is  (-∞, ∞)
• Range is [4, ∞)

Problem 3 :

f(x) = 3|x - 6|

Solution :

Comparing with y = a|x - h| + k

The minimum point or vertex is at (6, 0). Since a is positive the absolute value function opens up.

Slope = 3

Some of the points are (4, 6) (5, 3) (6, 0) (7, 3) and (8, 6).

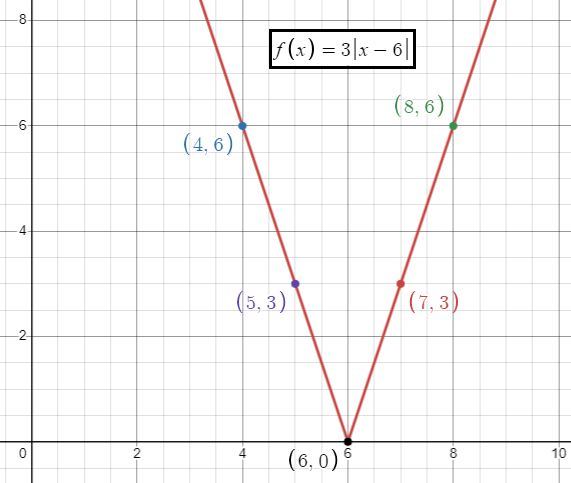
• Domain is all real values, that is  (-∞, ∞)
• Range is [0, ∞)

Problem 4 :

f(x) = -|x + 2| + 8

Solution :

Comparing with y = a|x - h| + k

The minimum point or vertex is at (-2, 8). Since a is positive the absolute value function opens down.

Slope = -1

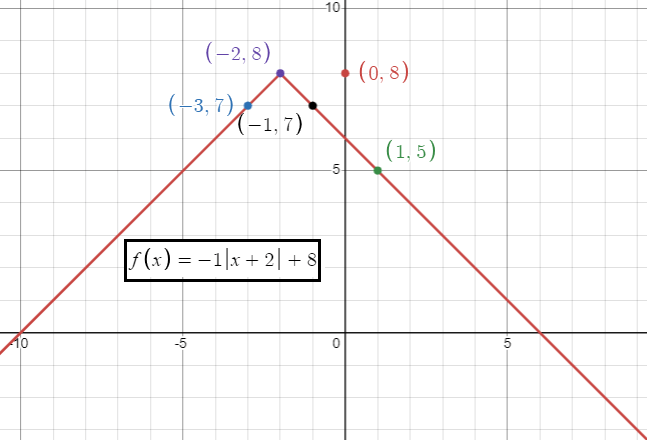
So, the points are (-3, 7) (-2, 8) (-1, 7) (0, 8) and (1, 5).

• Domain is all real values, that is  (-∞, ∞)
• Range is (-∞, 8]

Problem 5 :

f(x) = 2|-2(x - 1)| - 4

Solution :

Comparing with y = a|x - h| + k

The minimum point or vertex is at (1, -4). Since a is positive the absolute value function opens up.

Slope = 2

Some of the points on the absolute value function are (-2, 8)(-1, 4) (0, 0) (1, -4) and (2, 0).

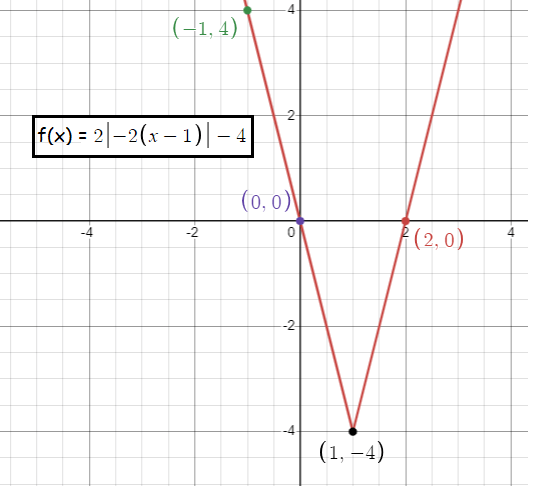
• Domain is all real values, that is  (-∞, ∞)
• Range is [-4, ∞)