TRIANGLES AND SPECIAL RIGHT TRIANGLES VOCABULARY WORDS
Right triangle :
A right angled triangle is a triangle with one of the angles as 90 degrees. A 90-degree angle is called a right angle.
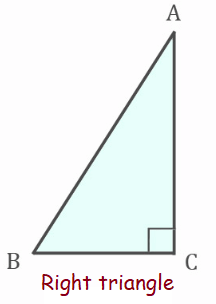
Definition of Leg :
A leg of a triangle is one of its sides. For a right triangle, the term "leg" generally refers to a side other than the one opposite the right angle (which is termed the hypotenuse).
AB is leg.
Hypotenuse :
The hypotenuse of a right triangle is always the side opposite the right angle. It is the longest side in a right triangle
AB is hypotenuse of the right triangle.
Pythagoras theorem :
Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“

AB2 = AC2 + BC2
Pythagorean triples :
Pythagorean triples are
a2+b2 = c2
where a, b and c are the three positive integers. These triples are represented as (a,b,c). Here, a is the perpendicular, b is the base and c is the hypotenuse of the right-angled triangle.
For example (9, 12 and 15) are Pythagorean triples.
152 = 92 + 122
225 = 81 + 144
225 = 225
Related Pages
- Find the missing side length using pythagorean theorem
- Word problems using pythagorean theorem worksheet
- Finding unknown length by pythagorean theorem
- Solving word problems on pythagorean theorem
- Find unknown in pythagorean triples
- Solving word problems using pythagorean theorem
- Solving word problems using pythagorean theorem worksheet
Special Right Triangles
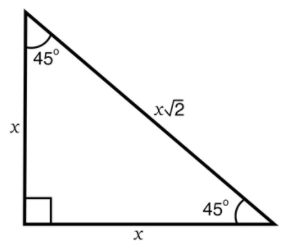
45-45-90 triangle :
The 45-45-90 triangle rule states that the three sides of the triangle are in the ratio 1:1:√2. So, if the measure of the two congruent sides of such a triangle is x each, then the three sides will be x, x and √2x.
This rule can be proved by applying the Pythagorean theorem.
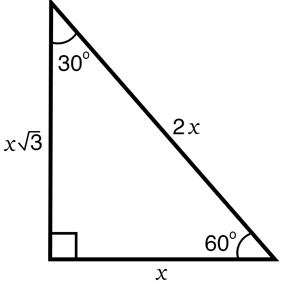
30-60-90 Theorem:
If a triangle has angle measures 30∘, 60∘ and 90∘, then the sides are in the ratio x : √3x : 2x .
The shorter leg is always be x
The side opposite to 90 degree is 2x
The side opposite to 60 degree is √3x
Related Pages
- Special right triangles
- SAT practice problems on special right triangles
- Special right triangles practice worksheet for SAT
- Finding the area of a regular polygon using special right triangles
- Practice problems on special right triangles
- Solving special right triangles with multi variables worksheet
- Solving special right triangles with multi variables
- Honors geometry practice problems in special right triangles
- Practice special right triangles for honors geometry
- Special right triangles practice worksheet honors geometry
Angle of elevation and depression
Trigonometric ratios :
The six trigonometric ratios are sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec).
Definition of sine :
The value of sin θ can be determined by dividing opposite side by hypotenuse.
sinθ = Opposite side / Hypotenuse
Definition of cosine :
The value of cos θ can be determined by dividing adjacent side by hypotenuse.
cos θ = Adjacent side / Hypotenuse
Definition of tangent :
The value of tan θ can be determined by dividing opposite side by adjacent side.
tan θ = Opposite side / Adjacent side
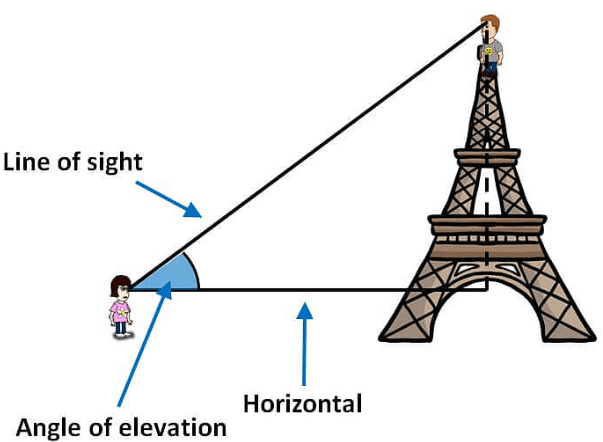
Angle of elevation :
The angle of elevation is formed when it is between the line of sight and the horizontal line. If the line of sight is above to the horizontal line, the angle formed is known as the angle of elevation. But in the angle of depression, the line of sight is downwards to the horizontal line. The figure that represents the angle of elevation is given below:
Angle of depression:
The angle of depression is the angle between the horizontal line and the observation of the object from the horizontal line. It is basically used to get the distance of the two objects where the angles and an object’s distance from the ground are known to us. Its an angle that is formed with the horizontal line if the line of sight is downward from the horizontal line.
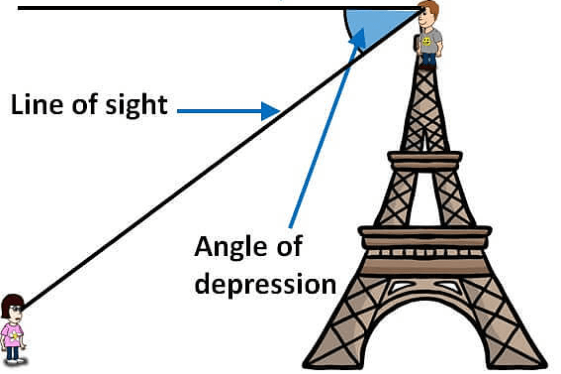
Related Pages
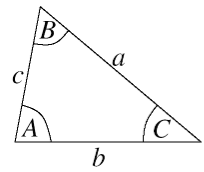
Law of Sines :
The Law of Sines is the relationship between the sides and angles of non-right (oblique) triangles . Simply, it states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all sides and angles in a given triangle.
Laws of Cosine :
The Cosine Rule can be used in any triangle where you are trying to relate all three sides to one angle.
a2 = b2 + c2 - 2bc cos A
b2 = a2 + c2 - 2ac cos B
c2 = a2 + b2 - 2ab cos C
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling