NUMBER OF SOLUTIONS TO A SYSTEM OF EQUATIONS ALGEBRAICALLY

The value which satisfies the given equation is known as solution. In general in system of equations, the point of intersection is known as solution.

The solution should lie on all lines involving in the problem.

There are three types of lines.

(i) Intersecting lines

(ii)  Parallel lines

(iii) Coincident lines

Intersecting lines :

There is one point of intersection, so it will have unique solution.

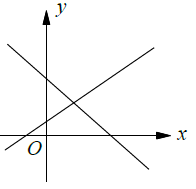
No solution :

The parallel lines will never meet. So, there is no point of intersection that is no solution.

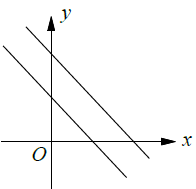
Parallel lines will have the same slope but different y-intercepts.

Infinitely many solution :

Two lines that lie exactly on top of each other or we can say that one line is exactly lying on top of another line are called coincident lines.

Coincident lines will have the same slope and same y-intercepts.

Problem 1 :

Tell how many solutions the linear system has :

infinitely many solutions, one solution, or no solution.

x - 4y = 2

2x - 8y = 5

Solution :

x - 4y = 2 ---> (1)

2x - 8y = 5 ---> (2)

Converting each equation in slope intercept form

y = mx + b (slope intercept form)

From (1)

x - 2 = 4y

4y = x - 2

y = x/4 - 2/4

m₁ = 1/4, b₁ = -1/2

From (2)

2x - 8y = 5

8y = 2x - 5

y = 2x/8 - 5/8

y = x/4 - 5/8

m₂ = 1/4, b₂ = -5/8

m₁ = m₂

Slopes are equal. So, they are parallel.

Hence, there are no solutions.

Problem 2:

Tell how many solutions the linear system has:

infinitely many solutions, one solution, or no solution.

x - 4y = 2

x + 4y = 2

Solution :

x - 4y = 2 ---> (1)

x + 4y = 2 ---> (2)

Converting each equation in slope intercept form

y = mx + b (slope intercept form)

From (1)

x - 2 = 4y

4y = x - 2

y = x/4 - 2/4

m₁ = 1/4, b₁ = -1/2

From (2)

x + 4y = 2

4y = -x + 2

y = -x/4 + 2/4

m₂ = -1/4, b₂ = 1/2

m₁ ≠ m₂

Slopes are different. So, there is one solution.

Problem 3 :

Is (5, -2) a solution of the system?

2x+6y = -2

x + 2y = 1

Solution :

2x+6y = -2 ---> (1)

x + 2y = 1---> (2)

Substitute x = 5, y = -2 in (1)

2(5) + 6(-2) = -2

10 - 12 = -2

-2 = -2

Substitute x = 5, y = -2 in (2)

5 + 2(-2) = 1

5 - 4 = 1

1 = 1

Yes. (5, -2) is a solution of the system.

Problem 4 :

Is (2, -1) a solution of the system?

2x + 6y = -2

x + 2y = 1

Solution :

2x + 6y = -2 ---> (1)

x + 2y = 1 ---> (2)

Substitute x = 2, y = -1 in (1)

2(2) + 6(-1) = -2

4 - 6 = -2

-2 = -2

Substitute x = 2, y = -1 in (2)

2 + 2(-1) = 1

2 - 2 = 1

0 = 1

No. (2, -1) is not a solution of the system.

Problem 5 :

The drama club sold 1500 tickets for the end of year performance. Admission prices were $12 for adults and $6 for students. The total amount collected at the box office was $15,600. Write the system of equations needed to solve.

Solution :

x + y = 1500 ---> (1)

12x + 6y = 15600 ---> (2)

From (1)

y = 1500 - x

Substitute y = 1500 - x in (2)

12x + 6(1500 - x) = 15600

12x + 9000 - 6x = 15600

6x + 9000 = 15600

6x = 15600 - 9000

6x = 6600

x = 1100