FIND COMPOSITION OF TWO FUNCTIONS

Composition of Two Composition

Problem 1 :

f(x) = -9x + 3 and g(x) = x⁴, find (f ∘ g)(x)

Solution :

(f ∘ g)(x) = f(g(x))

The function g(x) is input of the function f(x).

= f(x⁴)

= -9(x⁴) + 3

(f ∘ g)(x) = -9x⁴ + 3

• More problems on composition of functions
• Composition of square root function
• Finding composition of two functions worksheet
• Evaluate composition of functions for the given value

Composition of Function From Graph

Problem 2 :

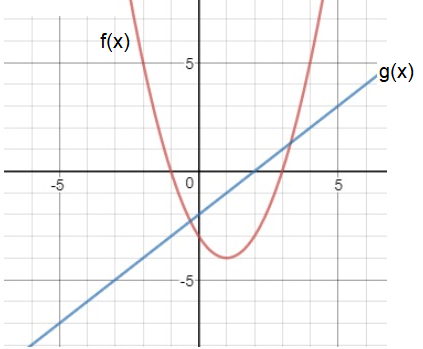
Use the graph of f(x) and g(x) to find the composition of functions.

 f(g(2))

Solution:

f(g(2))

From the graphs given above, it is clear that the line at x = 2  is crossing the curve g(x) at the point 0.

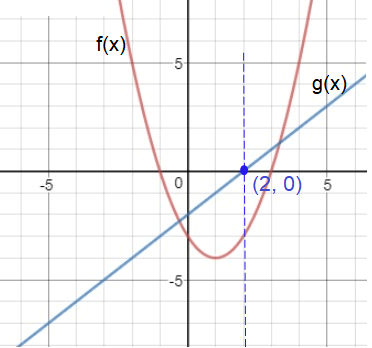
The value of g(2) is 0.

f(g(2)) = f(0)

When x = 0, the vertical line crosses the curve f(x) at -3.

f(g(2)) = -3

• More problems on composition of function from graph
• Composition of functions from a graph
• Composition of functions from a graph worksheet
• How to evaluate composition of function from graph

Composition from Table

Problem 3 :

Use the table of values to evaluate each expression

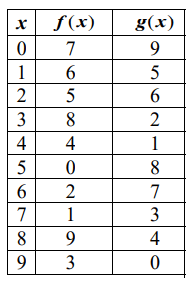
1)  f ( g(8) )     2)  f( g(5) )       3)  g ( f (5) )

Solution :

1)  f ( g(8) )

From the table, value of g(8) is 4.

f ( g(8) ) = f(4)

= 4

2)  f ( g(5) )

From the table, value of g(5) is 8.

f ( g(5) ) = f(8)

= 9

3)  g ( f (5) )

From the table, value of f(5) is 0.

g ( f(5) ) = f(0)

= 7

• Evaluating composition of functions from table
• Evaluating composition of functions from table worksheet

Composition from Arrow Diagram

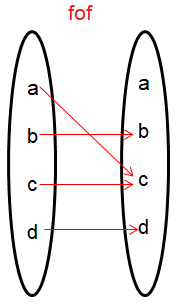
Problem 1 :

The arrow diagrams defines the functions

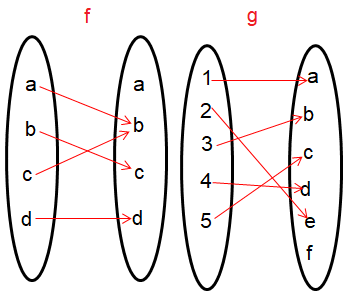
Find  f∘f  

i) f∘f :

Solution :

• Composition of functions from arrow diagram

Composition of Three Functions

Given f(x) = -2x + 1, g(x) = x², and h(x) = -1/2x + 1/2, evaluate the following:

Problem 4 :

Given f(x) = -2x + 1, find f(-6)

Solution:

f(x) = -2x + 1

f(-6) = -2(-6) + 1

= 12 + 1

f(-6) = 13

• Find more problems with three functions
• Composition of functions with three functions worksheet