ROTATION OF 2D SHAPES

Problem 1 :

Rotation 90° clockwise about the origin.

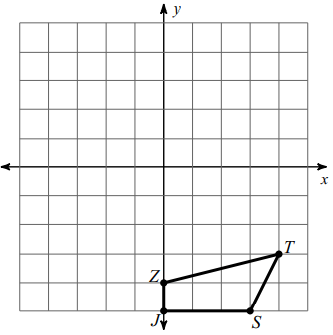
Solution :

Marking the coordinate,

Z (0, -4), J (0, -5), T (4, -3) and S (3, -5)

Rotation ==> 90° clockwise

Rule :

(x, y) ==> (y, -x)

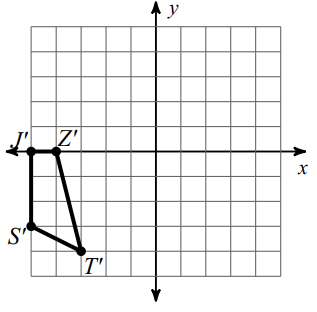
Z (0, -4) ==> Z' (-4, 0)

J (0, -5) ==> J' (-5, 0)

T (4, -3) ==> T' (-3, -4)

S (3, -5) ==> S'(-5, -3)

Problem 2 :

Rotation 180° clockwise about the origin.

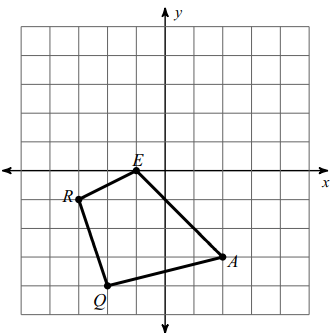
Solution :

Marking the coordinate,

E (-1, 0), R ( -3, -1), Q (-2, -4) and A (2, -3)

Rotation ==> 180°

Rule :

(x, y) ==> (-x, -y)

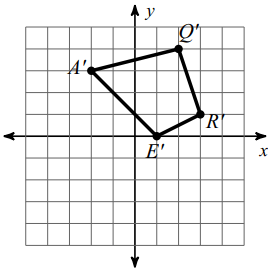
E (-1, 0) ==> E' (1, 0) 

R (-3, -1) ==> R' (3, 1)

Q (-2, -4) ==> Q' (2, 4)

A (2, -3) ==> A'(-2, 3)

Problem 3 :

Rotation 90° counter clockwise about the origin.

Solution :

Marking the coordinate,

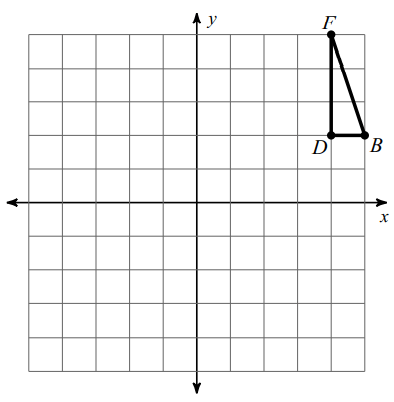
D (4, 2), F (4, 5) and B (5, 2).

Rotation ==> 90° counter clockwise

Rule :

(x, y) ==> (-y, x)

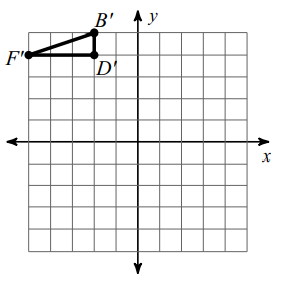
D (4, 2) ==> D' (-2, 4) 

F (4, 5) ==> F' (-5, 4)

B (5, 2) ==> B' (-2, 5)

Problem 4 :

Rotation 90° counter clockwise about the origin.

Solution :

Marking the coordinate,

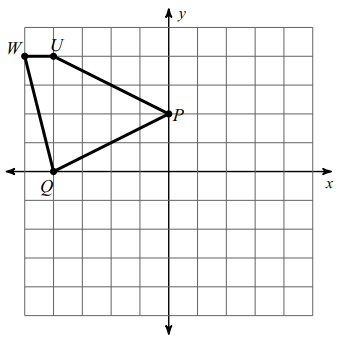
U (-4, 4), W (-5, 4), Q (-4, 0) and P (0, 2).

Rotation ==> 90° counter clockwise

Rule :

(x, y) ==> (-y, x)

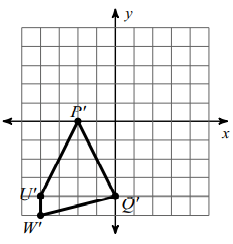
U (-4, 4) ==> U' (-4, -4) 

W (-5, 4) ==> W' (-4, -5)

Q (-4, 0) ==> Q' (0, -4)

P (0, 2) ==> P' (-2, 0)

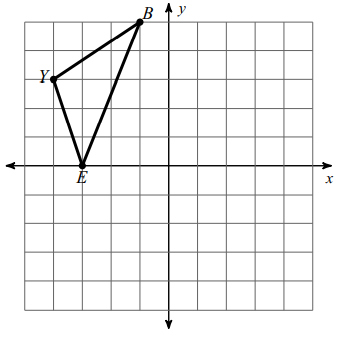
Problem 5 :

Rotation 180° about the origin.

Solution :

Marking the coordinate,

Y (-4, 3), B (-1, 5) and E (-3, 0)

Rotation ==> 180°

Rule :

(x, y) ==> (-x, -y)

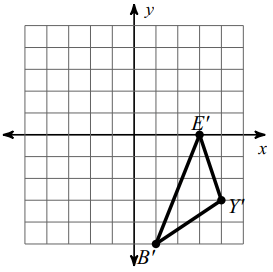
Y (-4, 3) ==> Y' (4, -3) 

B (-1, 5) ==> B' (1, -5)

E (-3, 0) ==> E' (3, 0)

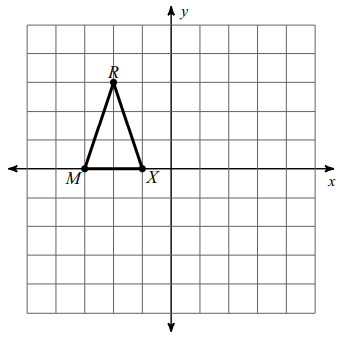
Problem 6 :

Rotation 90° clockwise about the origin.

Solution :

Marking the coordinate,

R (-2, 3), M (-3, 0) and X (-1, 0)

Rotation ==> 90° clockwise

Rule :

(x, y) ==> (y, -x)

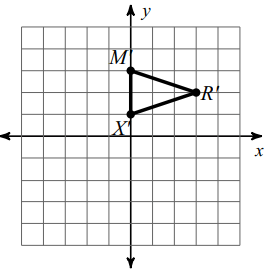
R (-2, 3) ==> R' (3, 2) 

M (-3, 0) ==> M' (0, 3)

X (-1, 0) ==> X' (0, 1)