ZEROES OF QUADRATIC POLYNOMIAL

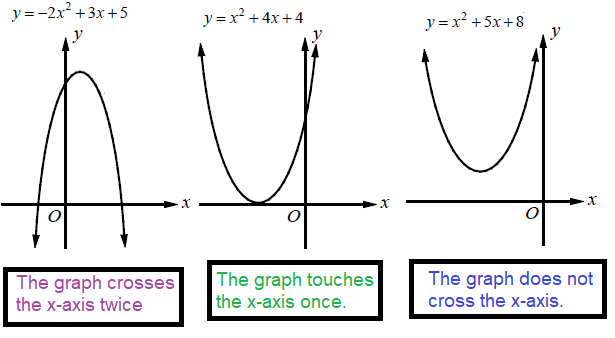
The solutions of a quadratic function are the values of x for which f(x) = 0. Solutions of functions are also called roots or zeros of the function.

On a graph, the solution of the function is the x-intercept(s).

Problem 1 :

Find zeroes of the quadratic polynomial

x² + x – 2 = 0

a. 4, -5       b. 2, -4       c. 2, -1      d.1, -2

Solution :

Given, x² + x – 2 = 0

x² – x + 2x – 2 = 0

x(x – 1) + 2(x – 1) = 0

(x + 2) (x – 1) = 0

x + 2 = 0 and x – 1 = 0

x = -2 x = 1

So, option (d) is correct.

Problem 2 :

Write a quadratic equation with the given roots. Write the equation in the form ax² + bx + c = 0, where a, b, and c are integers. 

-5 and -1

Solution :

The given values are solution. That is values of x.

x = -5 and x = -1

The factors are x + 5 and x + 1

Multiplying the factors, we get

f(x) = (x + 5)(x + 1) 

f(x) = x² + 5x + x + 5

f(x) = x² + 6x + 5

So, the required polynomial which are having two factors is 

f(x) = x² + 6x + 5

Problem 3 :

Write a quadratic polynomial, sum of whose zeroes is 2√3 and product is 5.

Solution :

Sum of zeroes = 2√3

Product of zeroes = 5

x² - (α + β)x + αβ = 0

x² - (Sum of zeroes)x + Product of zeroes = 0

x² - 2√3x + 5 = 0

Problem 4 :

For what value of k, (–4) is a zero of the polynomial

x² – x – (2k + 2)?

Solution :

Let f(x) = x² – x – (2k + 2)

Since -4 is zero of the polynomial,

f(-4) = 0

f(4) = 4² – 4 – (2k + 2) = 0

16 - 4 - 2k - 2 = 0

-2k + 10 = 0

-2k = -10

k = 5

So, the value of k is 5.

Problem 5 :

For what value of p, (–4) is a zero of the polynomial

x² – 2x – (7p + 3)?

Solution :

Let f(x) = x² – 2x – (7p + 3)

Since -4 is zero of the polynomial,

f(-4) = 0

f(4) = (-4)² – 2(-4) – (7p + 3) = 0

16 + 8 - 7p - 3 = 0

21 - 7p = 0

7p = 21

p = 3

So, the value of p is 3.

Problem 6 :

If 1 is a zero of the polynomial p(x) = ax² – 3(a – 1) x – 1, then find the value of a.

Solution :

Let p(x) = ax² – 3(a – 1) x – 1 

Since 1 is zero of the polynomial,

p(1) = a(1)² – 3(a – 1)(1) – 1 = 0

a - 3a + 3 - 1 = 0

-2a + 2 = 0

-2a = -2

a = 1

So, the value of a is 1.

Problem 7 :

If (x + a) is a factor of 2x² + 2ax + 5x + 10 find a.

Solution :

Let p(x) = 2x² + 2ax + 5x + 10

If x + a = 0, then x = -a. p(-a) = 0

p(-a) = 2(-a)² + 2a(-a) + 5(-a) + 10 = 0

2a² - 2a² - 5a + 10 = 0

-5a + 10 = 0

-5a = -10

a = 2

So, the value of a  is 2.