WRITING THE INVERSE TRIG FUNCTIONS AS ALGEBRAIC EXPRESSIONS

Write each trigonometric expression as an algebraic expression.

Problem 1 :

sin (csc^-1 x)

Solution :

Given, sin (csc^-1 x)

Using reference triangle.

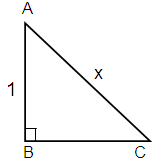
     Here Hypotenuse = x, Opposite = 1

Problem 2 :

sec (tan^-1 x)

Solution :

Given, sec (tan^-1 x)

Using reference triangle.

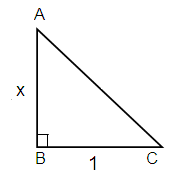
 Here Opposite = x, Adjacent = 1

AC² = AB² + BC²

= x² + 1²

Taking square root on each sides.

AC = √(x² + 1)

sec (tan^-1 x) = √(x² + 1)

Problem 3 :

cos (tan^-1 x)

Solution :

Given, cos (tan^-1 x)

Using reference triangle.

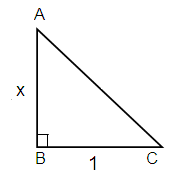
 Here Opposite = x, Adjacent = 1

AC² = AB² + BC²

= x² + 1²

Taking square root on each sides.

AC = √(x² + 1)

Problem 4 :

cot (sin^-1 x)

Solution :

Given, cot (sin^-1 x)

Using reference triangle.

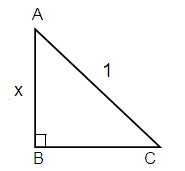
 Here Opposite = x, Hypotenuse = 1

AC² = AB² + BC²

1² = x² + BC²

1 - x² = BC²

Taking square root on each sides.

BC = √(1 - x²)

Problem 5 :

cot (cos^-1 x)

Solution :

Given, cot (cos^-1 x)

Using reference triangle.

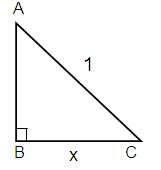
 Here Adjacent = x, Hypotenuse = 1

AC² = AB² + BC²

1² = AB² + x²

1 - x² = AB²

Taking square root on each sides.

AB = √(1 - x²)

Problem 6 :

cos (sin^-1 x)

Solution :

Given, cos (sin^-1 x)

Using reference triangle.

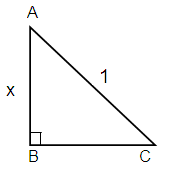
 Here Opposite = x, Hypotenuse = 1

AC² = AB² + BC²

1² = x² + BC²

1 - x² = BC²

Taking square root on each sides.

BC = √(1 - x²)

cos (sin^-1 x) = √(1 - x²)

Problem 7 :

Solution :

Using reference triangle.

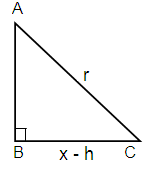
 Here Adjacent = x - h, Hypotenuse = r

AC² = AB² + BC²

r² = AB² + (x  - h)²

r² - (x - h)² = AB²

Taking square root on each sides.

AB = √(r² - (x - h)²)

Problem 8 :

Solution :

Using reference triangle.

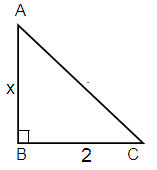
 Here Adjacent = 2, Opposite = x

AC² = AB² + BC²

AC² = x² + 2²

Taking square root on each sides.

AC = √(x² + 4)