WRITING EQUATION OF A TRANSFORMED FUNCTION

A translation is a  transformation  that shifts a graph  horizontally or  vertically, but  doesn’t change  the overall shape  or orientation.

Moving horizontally :

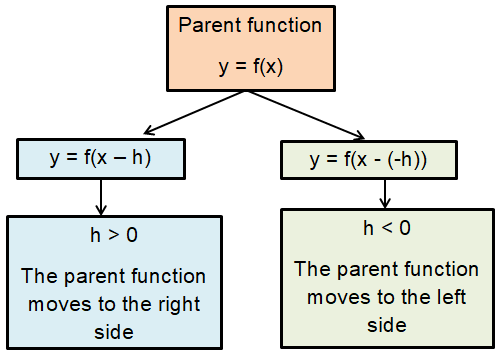
Moving vertically :

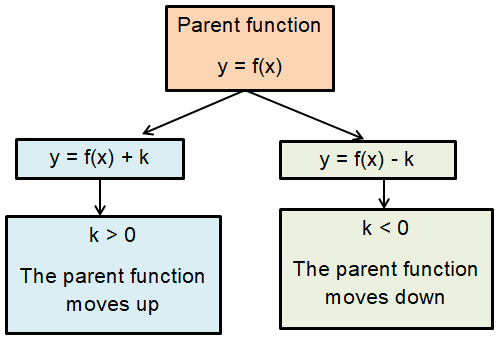
A dilation is a stretch or a compression.

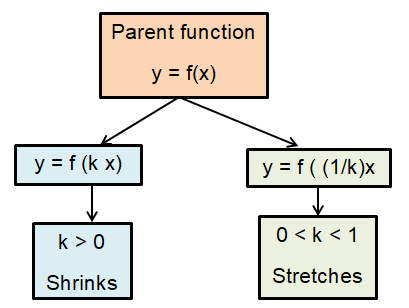
A reflection of a function is just the image of the curve with respect to either x-axis or y-axis.

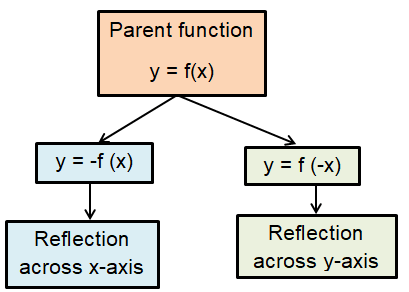
Write the function g whose graph represents the indicated transformation of the function f.

Problem 1 :

f(x) = 3x, translation 5 units up.

Solution :

Name of the transformation = Translation

Direction of translation = Moving vertically

Parent function = f(x) = 3x

After moving 5 units up :

f(x) = 3x + 5

Problem 2 :

f(x) = |x| - 3, translation 4 units to the right.

Solution :

Name of the transformation = Translation

Direction of translation = Moving horizontally

Parent function = f(x) = |x| - 3

After moving 4 units right :

f(x) = |x - 4| - 3

Problem 3 :

f(x) = -|x + 2| - 1 , reflection in the x-axis.

Solution :

Name of the transformation = Reflection

Reflection across axis = x-axis

Parent function = f(x) = -|x + 2| - 1

After reflection on x-axis :

f(x) = -f(x)

f(x) = -[-|x + 2| - 1]

f(x) = |x + 2| + 1

f(x) = |x + 2| + 1

Problem 4 :

f(x) = (1/2) x + 1, reflection in the y-axis.

Solution :

Name of the transformation = Reflection

Reflection across axis = y-axis

Parent function = f(x) = (1/2) x + 1

After reflection on y-axis :

f(x) = f(-x)

f(x) = (1/2)(-x) + 1

f(x) = (-1/2)x + 1

Problem 5 :

f(x) = x -  5, translation 4 units to the left.

Solution :

Name of the transformation = Translation

Direction of translation = Moving horizontally

Parent function = f(x) = x - 5

After moving 4 units to the left :

f(x) = (x -(- 4)) - 5

f(x) = (x + 4)) - 5

f(x) = x - 1

f(x) = x - 1

Problem 6 :

f(x) = x + 2, translation 2 units to the left.

Solution :

Name of the transformation = Translation

Direction of translation = Moving horizontally

Parent function = f(x) = x + 2

After moving 2 units to the left :

f(x) = (x - (-2)) + 2

f(x) = x + 4

Problem 7 :

f(x) = |4x+3| + 2, translation 2 units down.

Solution :

Name of the transformation = Translation

Direction of translation = Moving vertically

Parent function = f(x) = |4x+3| + 2

After moving 2 units down :

f(x) = |4x + 3| + 2 - 2

f(x) = |4x + 3|

Problem 8 :

f(x) = 2x - 9, translation 2 units up.

Solution :

Name of the transformation = Translation

Direction of translation = Moving vertically

Parent function = f(x) = 2x - 9

After moving 2 units up :

f(x) = 2x - 9 + 2

f(x) = 2x - 7