WRITING QUADRATIC EQUATIONS IN VERTEX FORM USING A GRAPH

Determine the equation of quadratic function from graph. Give the function in vertex form.

Example 1 :

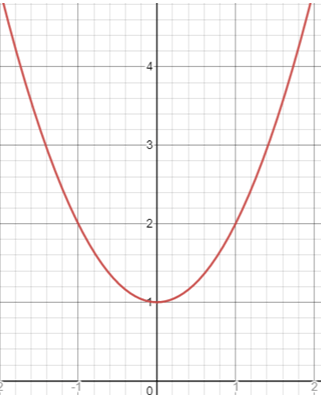
Solution :

The vertex is at (0, 1).

y = a(x - h)² + k

y = a(x - 0)² + 1----(1)

The parabola is passing through the point (1, 2).

2 = a(1 - 0)² + 1

2 - 1 = a(1 - 0)²

1 = a(1)

a = 1

By applying the value of a in (1), we get

y = 1(x - 0)² + 1

y = x² + 1

So, the equation of the parabola is y = x² + 1.

The coefficient of x² is 1, we see the evidence that the parabola opens up.

Example 2 :

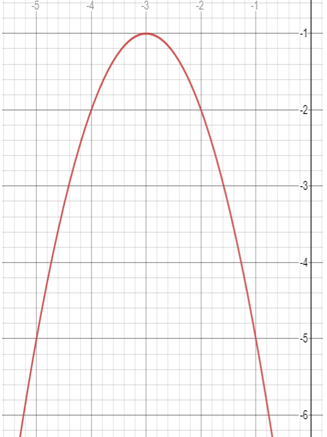
Solution :

The vertex is at (-3, -1).

y = a(x - h)² + k

y = a(x + 3)² - 1 ---(1)

The parabola is passing through the point (-2, -2).

-2 = a(-2 + 3)² - 1

-2 + 1 = a(1)²

1 = a

By applying the value of a in (1), we get

y = 1(x + 3)² - 1

So, the equation of the parabola is y = (x + 3)² - 1.

Example 3 :

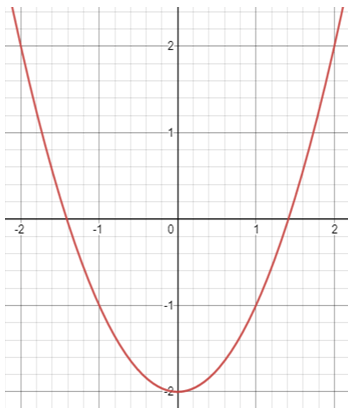
Solution :

The vertex is at (0, -2).

y = a(x - h)² + k

y = a(x + 0)² - 2 ---(1)

The parabola is passing through the point (-2, 2).

2 = a(-2 + 0)² - 2 

2 + 2 = a(-2)²

4 = 4a

a = 1

By applying the value of a in (1), we get

y = 1x² - 2

So, the equation of the parabola is y = x² - 2

Example 4 :

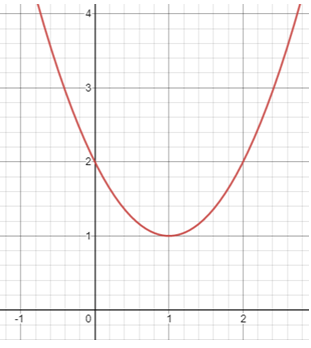
Solution :

The vertex is at (1, 1).

y = a(x - h)² + k

y = a(x - 1)² + 1 ---(1)

The parabola is passing through the point (0, 2).

2 = a(0 - 1)² + 1

2 - 1 = a(-1)² 

1 = a

By applying the value of a in (1), we get

y = 1(x - 1)² + 1

So, the equation of the parabola is y = 1(x - 1)² + 1.

Example 5 :

Which function represents the widest parabola? Explain your reasoning.

a) y = 2(x + 3)²        b)  y = x² − 5     c)  y = 0.5(x − 1)² + 1      d)  y = −x² + 6

Solution :

Option a :

y = 2(x + 3)² 

Vertex of the parabola is (-3, 0).

a = 2, vertical stretch of 2 units.

The graph should be narrower.

Option b :

y = x² − 5

Vertex of the parabola is (0, -5).

a = 1

There is no vertical stretch or compression.

Option c :

y = 0.5(x − 1)² + 1

Vertex of the parabola is (1, 1).

a = 0.5

Vertical compression of 0.5 units.

Graph should be wider.

Option d :

y = −x² + 6

Vertex of the parabola is (0, 6).

a = -1

There is no vertical stretch or compression.

So, option c is wider.

Example 6 :

The graph of which function has the same axis of symmetry as the graph of

y = x² + 2x + 2?

a) y = 2x² + 2x + 2       b)  y = −3x²− 6x + 2

c)  y = x² − 2x + 2       d)  y = −5 x²+ 10x + 2

Solution :

y = x² + 2x + 2

To find axis of symmetry, we have to express the given quadratic functions in vertex form using the method of completing the square.

y = x² + 2x(1) + 1² - 1² + 2

y = (x + 1)² - 1² + 2

y = (x + 1)² - 1 + 2

y = (x + 1)² + 1

Axis of symmetry is x = -1

So, option v us correct.

Option a :

y = 2x² + 2x + 2 

y = 2(x² + 1x) + 2 

y = 2[x² + 2 (1/2)x + (1/2)² - (1/2)²] + 2

y = 2[(x + 1/2)² - (1/4)] + 2

y = 2(x + 1/2)² - (2/4) + 2

y = 2(x + 1/2)² - (1/2) + 2

y = 2(x + 1/2)² + (3/2)

Axis of symmetry is x = -1/2

Option a :

y = −3x²− 6x + 2

y = -3(x² + 2x) + 2 

y = -3[x² + 2 x(1) + 1² - 1²] + 2

y = -3[(x + 1)² - 1] + 2

y = -3(x + 1)² + 3 + 2

y = -3(x + 1)² + 5

Axis of symmetry is x = -1

So, option b is correct.

Example 7 :

The path of a diver is modeled by the function

f(x) = −9x² + 9x + 1

where f(x) is the height of the diver (in meters) above the water and x is the horizontal distance (in meters) from the end of the diving board.

a. What is the height of the diving board?

b. What is the maximum height of the diver?

c. Describe where the diver is ascending and where the diver is descending.

Solution :

f(x) = −9x² + 9x + 1

a) height of the board is 1 meter.

b) To find the height of the diving boards, we have to write the function in vertex form,

f(x) = −9(x² - x) + 1

= −9[x² - 2 x(1/2) + (1/2)² - (1/2)²] + 1

= −9[(x - 1/2)² - (1/4)] + 1

= −9(x - 1/2)² + (9/4) + 1

= −9(x - 1/2)² + (13/4)

Reaches the maximum height at 0.5 seconds and the height is 3.25 m

c) When x > 0.5, it is increasing and x < 0.5 it is decreasing.