WRITING POLYNOMIALS IN DIVISOR TIMES QUOTIENT PLUS REMAINDER FORM

Problem 1 :

The equation 

is true for all values of x ≠ 2/3, where k is a constant. What is the value of k ?

(a)  8       (b)  9     (c)  11     (d)  15

Solution :

So, the value of k is 15.

Problem 2 :

Where a, b and c are constants. What is the value of a + b + c ?

Solution :

Comparing the coefficient of x², x and constants.

a = 3

b - a = 1  ----(1)

c - b = 2 -----(2)

Applying the value of a in (1), we get

b - 3 = 1

b = 4

Applying the value of b in (2), we get

c - 4 = 2

c = 6

a + b + c = 3+4+6

= 13

So, the answer is 13.

Problem 3 :

In the following find the value of R

Solution :

Comparing constants :

3 = R - 3

R = 3 + 3

R = 6

Alternative way :

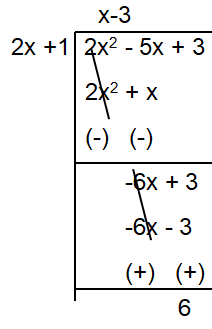
So, the value of R is 6.

Problem 4 :

In the equation above, a is a constant and ax − 1 ≠ 1. What is the value of a ?

Solution :

Comparing the coefficients of x, we get

-7 + 8a = 9

8a = 9 + 7

8a = 16

a = 2

Problem 5 :

From the information given below, find the value A.

Solution :

Comparing constants, we get

4 = 1 + A

A = 3

Problem 6 :

In the following, find the value of a.

Solution :

Comparing constants, the value of a is 6.

Problem 7 :

In the following, find the value of A.

Solution :

Comparing the constant terms, we get

10 = 12 - A

A = 12 - 10

A = 2