WRITING INTERVAL NOTATION GIVEN A NUMBER LINE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
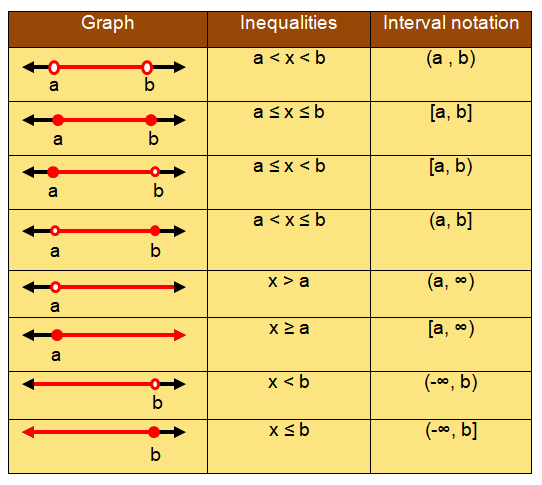
Interval Notation :
Interval notation is a method to represent an interval on a number line. In other words, it is a way of writing subsets of the real number line.
An interval comprises the numbers lying between two specific given numbers.
Use interval notation to describe :
Problem 1 :

Solution :
By observing the number line, the possible values of x are
-2 ≤ x < 1
By expressing it as interval notation, we get
[-2, 1)
Problem 2 :

Solution :
By observing the number line, the possible values of x are
x ≤ 0 or x > 1
By expressing it as interval notation, we get
(-∞, 0] and (1, ∞)
Problem 3 :

Solution :
By observing the number line, the possible values of x are
2 ≤ x ≤ 4
By expressing it as interval notation, we get
[2, 4]
Problem 4 :

Solution :
By observing the number line, the possible values of x are
-2 < x < 1
By expressing it as interval notation, we get
(-2, 1)
Problem 5 :

Solution :
By observing the number line, the possible values of x are
x < -1 (or) x > 1
By expressing it as interval notation, we get
(-∞, -1) and (1, ∞)
Problem 6 :

Solution :
By observing the number line, the possible values of x are
0 < x ≤ 4
By expressing it as interval notation, we get
(0, 4]
Problem 7 :

Solution :
By observing the number line, the possible values of x are
x < 0 (or) x ≥ 3
By expressing it as interval notation, we get
(-∞, 0) and [3, ∞)
Problem 8 :

Solution :
By observing the number line, the possible values of x are
x ≤ -2 (or) x ≥ 2
By expressing it as interval notation, we get
(-∞, -2] and [2, ∞)
Problem 9 :

Solution :
By observing the number line, the possible values of x are
x < -2 (or) 1 < x ≤ 4
By expressing it as interval notation, we get
(-∞, -2) and (1, 4]
Problem 10 :
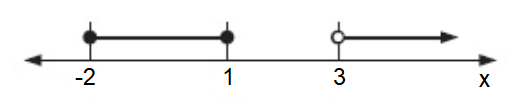
Solution :
By observing the number line, the possible values of x are
-2 ≤ x ≤ 1 (or) x > 3
By expressing it as interval notation, we get
[-2, -1] and (3, ∞)
Problem 11 :
The water temperature of a swimming pool must be no less than 76°F. The temperature is currently 74°F. Which graph correctly shows how much the temperature needs to increase? Explain your reasoning.
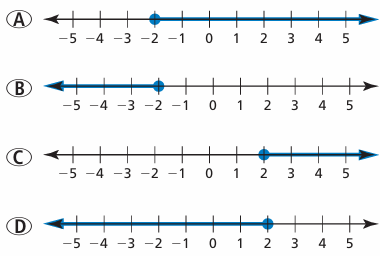
Solution :
Let x be the temperature.
The temperature is no less than 76°F, then x ≥ 76
Current temperature = 74°F
So, we have to increase atleast 2°F. Option C is correct.
Problem 12 :
According to a state law for vehicles traveling on state roads, the maximum total weight of a vehicle and its contents depends on the number of axles on the vehicle. For each type of vehicle, write and graph an inequality that represents the possible total weights w (in pounds) of the vehicle and its contents.

Solution :
The inequalities that represent the maximum weights are:
- 2 axles - x ≤ 40000
- 3 axles - x ≤ 60000
- 4 axles - x ≤ 80000
Let the maximum weight be represented with x
In inequality, maximum means less than or equal to i.e. ≤
(a) 2 axles
The maximum weight, here is 40000.
So, the inequality is:
x ≤ 40000
(b) 3 axles
The maximum weight, here is 60000.
So, the inequality is:
x ≤ 60000
(c) 4 axles
The maximum weight, here is 80000.
So, the inequality is:
x ≤ 80000
Problem 13 :
The graph represents the known melting points of all metallic elements (in degrees Celsius).

a. Write an inequality represented by the graph.
b. Is it possible for a metallic element to have a melting point of −38.87°C? Explain.
Solution :
a) Let x be the temperature.
Since we have solid circle, we have to use the less than or equal to greater than or equal sign.
x ≥ -38.87
b) Yes, it is possible for a metallic element to have a melting point of -38.87 because this is the melting point of the metallic element mercury.
Problem 14 :
write an inequality that represents the missing dimension x.
The area is less than 42 square meters.
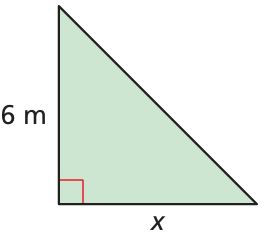
Solution :
Base = x meter and height = 6 m
Area of triangle = (1/2) • base • height
= (1/2) • x • 6
= 3 x
Area of the triangle is less than 42 square meter.
3x < 42
Solving for x, we get
x < 42/3
x < 14
Problem 15 :
The area is greater than or equal to 8 square feet
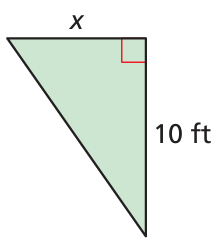
Solution :
Base = x ft and height = 10 ft
Area of triangle = (1/2) • base • height
= (1/2) • x • 10
= 5 x
Area of the triangle is greater than 8 square feet
5x > 8
Solving for x, we get
x > 8/5
Problem 16 :
The area is less than 18 square centimeters.
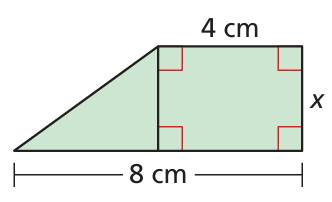
Solution :
Total area = area of triangle + area of rectangle
= (1/2) • 4 • x + 4 • x
= 2x + 4x
= 6x
Area is less than 18 square cm
6x < 18
x < 18/6
x < 3
Problem 17 :
The area is greater than 12 square inches
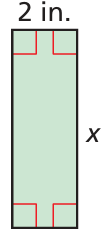
Solution :
Length = 2 inches and width = x inches
Area of rectangle > 12
2x > 12
x > 12/2
x > 6
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling