WRITING EXPRESSIONS WITHOUT ABSOLUTE VALUE SIGNS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Using |a | = a if a ≥ 0 and –a if a < 0, write the following functions without modulus signs and hence graph each function :
Problem 1 :
y = |x – 2|
Solution :
Step 1 :
If x ≥ 2, then (x – 2) ≥ 0
If x < 2, then (x – 2) < 0, that is -(x - 2).
Step 2 :
Simplifying the second branch -(x - 2), we get
-x + 2 or 2 - x
Step 3 :
Removing the absolute sign, we get piecewise functions given below.
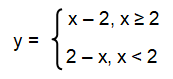
Problem 2 :
y = |x + 1|
Solution :
Step 1 :
If x ≥ -1, then (x + 1) ≥ 0
If x < -1, then (x + 1) < 0, that is -(x + 1).
Step 2 :
Simplifying the second branch -(x + 1), we get
-x - 1
Step 3 :
Removing the absolute sign, we get piecewise functions given below.
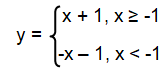
Problem 3 :
y = - |x|
Solution :
Step 1 :
If x ≥ 0, then y = -x
If x < 0, then y = -(-x)
Step 2 :
Simplifying the second branch -(-x), we get
y = x
Step 3 :
Removing the absolute sign, we get piecewise functions given below.
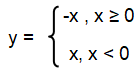
Problem 4 :
y = |x| + x
Solution :
Step 1 :
If x ≥ 0, then y = x + x
If x < 0, then y = (-x) + x
Step 2 :
Simplifying the second branch -(-x), we get
y = (-x) + x
y = 0
Step 3 :
Removing the absolute sign, we get piecewise functions given below.
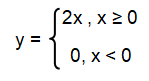
Problem 5 :
y = |x|/x
Solution :
Step 1 :
If x > 0, then y = x/x
If x < 0, then y = (-x)/x
If x = 0, then y = undefined
Step 2 :
- By simplifying y = x/x, we get y = 1
- By simplifying y = -x/x, we get y = -1
Step 3 :
Removing the absolute sign, we get piecewise functions given below.
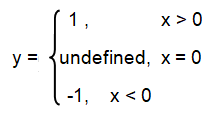
Problem 6 :
y = x - 2 |x|
Solution :
Step 1 :
If x ≥ 0, then y = x - 2x
If x < 0, then y = x - 2(-x)
Step 2 :
- By simplifying y = x - 2x, we get y = -x
- By simplifying y = x - 2(-x), we get y = x + 2x ==>y = 3x
Step 3 :
Removing the absolute sign, we get piecewise functions given below.
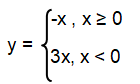
Problem 7 :
y = |x| + |x – 2|
Solution :
Step 1 :
By decomposing y = |x| + |x - 2| into two branches, we get
x + x – 2 and –x – (x – 2)
Step 2 :
Simplifying x + x – 2, we get 2x – 2.
Simplifying -x -(x – 2), we get –x –x + 2, that is 2 – 2x.
Step 3 :
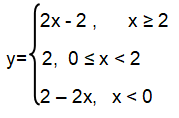
Problem 8 :
y = |x| - |x - 1|
Solution :
Step 1 :
By decomposing y = |x| - |x - 1| into two branches, we get
x - x – 1 and –x – (-x – 1)
Step 2 :
Then, x - x – 1, that is -1 and –x – (-x – 1) will become –x + x + 1, that is 1.
Step 3 :
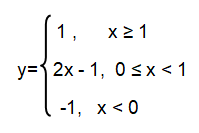
Problem 9 ;
y = |x2 + 1|
Solution :
Step 1 :
By decomposing |x2 + 1| into two branches, we get
x2 + 1 and –x2 - 1
y = |x2 + 1| for all x.
Problem 10 ;
y = |x2 - 1|
Solution :
Step 1 :
By decomposing |x2 - 1| into two branches, we get
x2 - 1 and –(x2 – 1)
Step 2 :
Then, -(x2 –
1) will become –x2 + 1, that is 1 - x2.
Step
3 :
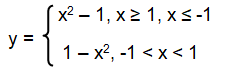
Problem 11 :
y = |x2 – 2x|
Solution :
Step 1 :
By decomposing |x2 – 2x | into two branches, we get
x2 – 2x and –(x2 – 2x)
Step 2 :
Then, -(x2 – 2x) will become –x2 + 2x, that is 2x - x2.
Step 3 :
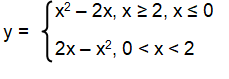
Problem 12 :
y = |x2 + 3x + 2|
Solution :
Step 1 :
By decomposing |x2 + 3x + 2| into two branches, we get
x2 + 3x + 2 and –(x2 + 3x + 2)
Step 2 :
Then, -(x2 + 3x + 2) that is –x2 - 3x – 2.
Step 3 :
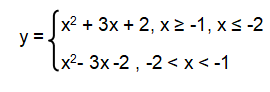
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling