WRITING EQUATIONS WITH INDEPENDENT AND DEPENDENT VARIABLES

What's a independent variable?

An independent variable is exactly what it sounds like. It is a variable that stands alone and isn't changed by the other variables you are trying to measure.

What's a dependent variable?

Just like an independent variable, a dependent variable is exactly what it sounds like. It is something that depends on other factors.

Problem 1 :

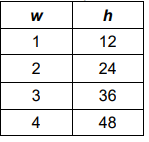
The table shows the relationship between the age of a plant in weeks, w, and the height of the plant in cm, h. Write an equation to represent this relationship.

Solution :

When w = 1, h = 12

When w = 2, h = 24

When w = 3, h = 36

When w = 4, h = 48

h = 12w

Problem 2 :

Using the table above, predict the plant’s height in cm when it is 8 weeks old

Solution :

h = 12w

Here w is number of weeks, when w = 8

h = 12(8)

h = 96 cm

Problem 3 :

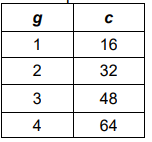
The table shows the relationship between the number of cups, c, and the number of gallons, g. Write an equation to represent this relationship. Also find,

i)  How many gallons will 128 cups make?

Solution :

When g = 1, c = 16

When g = 2, c = 32

There is constant change, 32 / 16 = 2

c = 16g, where g = 1, 2, 3, ............

i) Number of cups made, when g = 128

128 = 16g

g = 128/16

g = 8

Problem 4 :

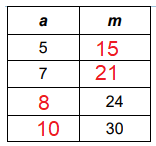
The following table represents the equation m = 3a. Fill in the missing values.

Solution :

m = 3a

When a = 5, m = 3(5) ==> 15

When a = 7, m = 3(7) ==> 21

When m = 24 and m = 30

Applying the values of m in m = 3a, we get

Problem 5 :

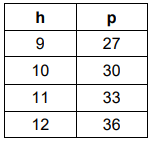
The table shows the relationship between the pounds of dough prepared, p, and the number of hours worked, h. Write an equation to represent this relationship. Also find

i) Predict how many pounds of dough will be prepared after 24 hours.

Solution :

by observing the table of values of h and p, h is being multiplied by 3.

p = 3h, where h = 9, 10, 11, ...

i) When h = 24, p = ?

p = 3(24)

p = 72

72 pounds of dough has been prepared.

Problem 6 :

The table shows the relationship between the minutes Vanessa spends walking, m, and the number of laps around the track she completes, c. Write an equation to represent this relationship.

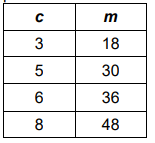
i)  If she keeps walking at this rate, how many laps will she have completed after 72 minutes?

Solution :

By observing the table of values of c and m,

m = 6c, where h = 3, 4, 5, ...

i) When m = 72

72 = 6c

c = 72/6

c = 12

She will complete 12 laps.

Problem 7 :

The following table represents the equation y = x - 4. Fill in the missing values.

Solution :

Given equation : y = x - 4

Problem 8 :

Ella's birthday party costs $3 for every guest she invites. Write an equation that shows the relationship between the guests, g, and the cost, c. Then complete the table.

Solution :

g = number of guests and c = cost

c = 3g