WRITING EQUATIONS FOR PROPORTIONAL RELATIONSHIPS WORD PROBLEMS

Problem 1 :

John and Amber work at an ice cream shop. The hours worked and wages earned are given for each person.

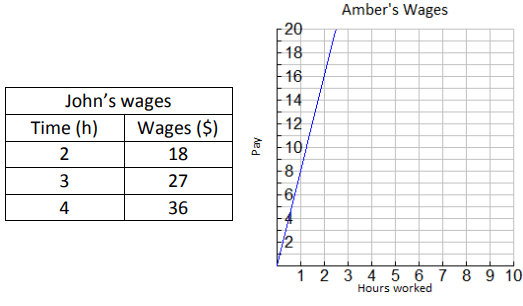
a) Are John’s wages proportional to time. How do you know? If they are, determine the unit rate.

b) Are Amber’s wages proportional to time. How do you know? If they are, determine the unit rate.

c) Write an equation to model the relationship between each person’s wages. Identify the constant of proportionality for each.

d) How much would each worker make after working 10 hours? Who will earn more money?

Solution :

a)  Time (x) = independent variable

Wages (y) = Dependent variable

When time = 2, wages = $18

Constant of proportionality (k) = 18/2 ==> 9

Let us check if the same rate maintains.

When x = 3, y = 27

k = 27/3 ==> 9

y = 9x ----(1)

So, John's wage is proportional to time.

b) Amber's wage :

Choosing two points (1, 8) and (2, 16)

k = 8/1 ==> 8

k = 16/2 ==> 8

y = 8x ----(2)

c) Constant of proportionality from John's wage = 9

Constant of proportionality from Amber's wage = 8

d)  

John is earning more.

Problem 2 :

It cost $5 to send 6 packages through a certain shipping company. Consider the number of packages per dollar.

a)  Find the constant of proportionality for this situation.

b)  Write an equation to represent the relationship.

Solution :

Number of package (x) - independent variable

Cost of packages (y) = dependent variable

Cost of 6 packages = $5

Cost of 1 package = 5/6

a) Constant of proportionality = 5/6

b) Equation of this relation ship will be in the form y = kx

y = (5/6)x

Problem 3 :

Write an equation that will model the proportional relationships shown in the graph below graph.

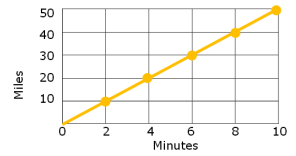
Solution :

Number of minutes (x) = Independent variable

Miles covered (y) = Dependent variable

In 2 minutes, he can cover 20 miles

unit rate = 20/2 ===> 2

Equation of the relationship y = 2x

Problem 4 :

Jennifer is shopping with her mother. They pay $2 per pound for tomatoes at the vegetable stand.

a) Write an equation to represent the proportional relationship.

b) How much will Jennifer pay if she buys 5.3 pounds of tomatoes?

Solution :

Defining independent and dependent variable :

Quantity of tomato = x = independent variable

Total cost = y = dependent variable

Cost of 1 pound of tomato = $2

Let x be the number of pounds of tomatoes

y be the total cost.

a) y = 2x

b) When x = 5.3 pounds

y = 2(5.3)

y = $10.6

Problem 5 :

In Katya's car, the number of miles driven is proportional to the number of gallons of gas used. Find the missing value in the table.

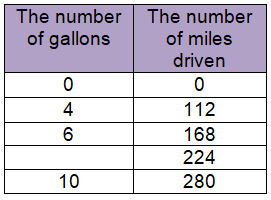
a) Write an equation that will relate the number of miles driven  to the number of gallons of gas.

b) What is the constant of proportionality ?

c) How many miles could Katya go if she filled her 22 gallon tank ?

d)  If Katya takes a trip of 600 miles, how many gallons of gas would be needed to make the trip ?

e) If Katya drives 224 miles during one week of commuting to school and work, how many gallons of gas would she use ?

Solution :

Independent variable (x) = number of gallons

Dependent variable (y) = Number of miles driven

Constant of proportionality (k) = y/x

k = 112/4

k = 28

a) y = 28x

b) Constant of proportionality k = 28

c) When x = 22

y = 28(22)

y = 616

d) When y = 660 miles

660 = 28x

x = 660/28

x = 23.57

e) y = 28x

When y = 224

224 = 28x

x = 224/28

x = 8

So, she will use 8 gallons.