WRITING COMPLEX NUMBER IN POLAR FORM
The length of the line segment, that is OP, is called the modulus of the complex number. The angle from the positive axis to the line segment is called the argument of the complex number, z.
Example :
Find the modulus and argument of a complex number
1 + i
Solution :
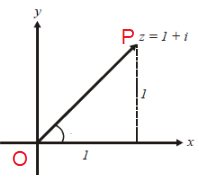
Finding Modulus :
Sum of squares of real part and imaginary part.
|
Modulus : OP = |z| = √12 + 12 OP = √2 |
Argument : θ = tan-1(y/x) θ = tan-1(1/1) θ = tan-1(1) θ = π/4 |
In the argant plane, angle lies in the
|
1st quadrant 2nd quadrant 3rd quadrant 4th quadrant |
θ = α θ = π - α θ = -π + α θ = - α |
Polar form :
r (cos θ + i sin θ)
Plot the following points on a plane and evaluate their polar forms :
Problem 1 :
z = -1 + 2i
Solution :
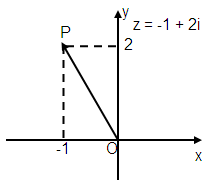
|
Modulus : OP = |z| = √(-1)2 + (2)2 = √(1 + 4) = √5 |
Argument : α = tan-1(y/x) α = tan-1(2/-1) α = tan-1(2) |
Converting the complex number as ordered pair, we get (-1, 2). So, the complex number will lie in the second quadrant.
θ = π - α
r = √5 and θ = π-tan-1(2)
√5(cos (π - tan-1(2)) + i sin (π - tan-1(2)))
Write the complex number in polar form.
Problem 2 :
z = -3 - 3i
Solution :
|
Modulus : r = |-3 - 3i| = √(-3)2 + (-3)2 = √(9 + 9) = √18 r = 3√2 |
Argument : α = tan-1(y/x) α = tan-1(-3/-3) α= tan-1(1) = π/4 |
Converting the complex number as ordered pair, we get (-3, -3). So, the complex number will lie in the third quadrant.
θ = -π + α
So, the principal value θ = -π + π/4
= (-4π + π)/4
= -3π/4
r = 3√2 and θ = -3π/4
So, the required polar form will be :
3√2(cos (-3π/4) + i sin (-3π/4))
Problem 3 :
z = 3 - 4i
Solution :
|
Modulus : r = |3 - 4i| = √(3)2 + (-4)2 = √(9 + 16) = √25 r = 5 |
Argument : α = tan-1(y/x) α = tan-1(-4/3) |
Converting the complex number as ordered pair, we get (3, -4). So, the complex number will lie in the fourth quadrant.
θ = -α
θ = -tan-1(4/3)
So, the required polar form will be :
Here r = 5 and θ = -tan-1(4/3)
5(cos (-tan-1(4/3)) + i sin (-tan-1(4/3)))
Problem 4 :
z = 2i
Solution :
|
Modulus : r = |0 + 2i| = √(2)2 = √4 r = 2 |
Argument : θ = tan-1(y/x) θ = tan-1(2/0) = tan-1 (∞) = π/2 |
Converting the complex number as ordered pair, we get (0, 2). So, the principal value θ = π/2
So, the required polar form will be :
Here r = 2 and θ = π/2
2(cos (π/2) + i sin (π/2))
Problem 5 :
z = 3
Solution :
|
Modulus : r = |3 + 0i| = √(3)2 r = 3 |
Argument : θ = tan-1(y/x) θ = tan-1(0/3) = 0 |
Converting the complex number as ordered pair, we get (3, 0). So, the principal value θ = 0
So, the required polar form will be :
So, the principal value θ = 0
So, the required polar form will be :
Here r = 3 and θ = 0
3(cos 0 + i sin 0)
Problem 6 :
z = -4
Solution :
|
Modulus : r = |-4 + 0i| = √(-4)2 r = 4 |
Argument : α = tan-1(y/x) α = tan-1(0/-4) = 0 |
Since, the complex number -4 has a negative, z lies in the third quadrant. Then, θ = π - α
θ = π - 0 ==> π
So, the required polar form will be :
Here r = 4 and θ = π
4(cos π + i sin π)
Problem 7 :
z = -5i
Solution :
|
Modulus : r = |0 - 5i| = √(-5)2 = √25 r = 5 |
Argument : α = tan-1(y/x) α = tan-1(-5/0) = -tan-1 (∞) = -π/2 |
The complex number is in the form (0, -5)
So, the required polar form will be :
Here r = 5 and θ = -π/2
4(cos (-π/2) + i sin (-π/2))
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling