WRITING AND SOLVING EQUATIONS FROM WORD PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
- Let us assume the unknown as x.
- Create the equation by understanding the situation. To solve the equation, we follow the steps given below.
- Distribute to get rid of the parentheses, if necessary.
- Combine like terms on the same side of the “=”.
- Add & subtract to get all constants to one side of the “=” and all variables to the other side of the “=”.
- Multiply & Divide to get the variable by itself.
- Check using substitution
Convert the following statements into equations and solve it.
Problem 1 :
5 added to a number is 9.
Solution :
Let x be the required number.
5+x = 9
Subtract 5 on both sides, we get
x = 9-5
x = 4
So, the required number is 4.
Problem 2 :
3 subtracted from a number is equal to 12.
Solution :
Let x be the required number.
x-3 = 12
Add 3 on both sides.
x = 12+3
x = 15
So, the required number is 15.
Problem 3 :
5 times a number decreased by 2 is 4.
Solution :
Let x be the required number.
5x-2 = 4
Add 2 on both sides.
5x = 4+2
5x = 6
Divide by 5 on both sides.
x = 4/5
Problem 4 :
2 times the sum of the number x and 7 is 13.
Solution :
Let x be the required number,
2x+7 = 13
Subtract 7 on both sides.
2x = 13-7
2x = 6
Divide by 2 on both sides.
x = 6/2
x = 3.
Problem 5 :
A number is 12 more than the other. Find the numbers if their sum is 48.
Solution :
Let x and y be two numbers.
x = 12+y
The sum of the numbers = 48
x+y = 48
12+y+y = 48
12+2y = 48
Subtract 12 on both sides.
2y = 48-12
2y = 36
Divide by 2 on both sides.
y = 36/2
y = 18
Problem 6 :
Twice the number decreased by 22 is 48. Find the number.
Solution :
Let x be the number
Twice a number = 2x
2x-22 = 48
Add 22 on both sides.
2x = 48+22
2x = 70
Dividing by 2.
x = 70/2
x = 35
Problem 7 :
Seven times the number is 36 less than 10 times the number. Find the number.
Solution :
7x-36 = 10x
7x-10x = 36
3x = 36
Dividing by 3, we get
x = 36/3
x = 12
Problem 8 :
The sum of two consecutive even number is 38. Find the numbers.
Solution :
Let x be the first even number. Its consecutive even number be x+2.
Sum of the even numbers = 38
x+(x+2) = 38
2x + 2 = 38
Subtract 2 on both sides, we get
2x = 38-2
2x = 36
Divide by 2 on both sides.
x = 36/2
x = 18
18 and 20 are required two consecutive even numbers.
Problem 8 :
The sum of three consecutive odd numbers is 51. Find the numbers.
Solution :
Let x be the first odd number.
x, x+2, x+4 are three consecutive odd numbers.
Sum of those three numbers = 51
x+(x+2)+(x+4) = 51
3x + 6 = 51
Subtract 6 on both sides.
3x = 51-6
3x = 48
Divide by 3 on both sides.
x = 48/3
x = 16
Problem 9 :
Rene is 6 years older than her younger sister. After 10 years, the sum of their ages will be 50 years. Find their present ages.
Solution :
Let x be Rene's younger sister's age.
Rene's age = x-6
After 10 years :
Rene's age = x-6+10 ==> x+4
Age of her younger sister = x+10
Rene's age + Her younger sister's age = 50
(x+4)+(x+10) = 50
2x+14 = 50
2x = 50-14
2x = 36
x = 18
Problem 10 :
A length of a rectangle is 10 cm more than its width. If the perimeter of the rectangle is 80 cm, find the dimensions of the rectangle.
Solution :
Let x be the width of the rectangle.
Length = x+10
Perimeter of the rectangle = 80
2(l+w) = 80
l+w = 40
x+10+x = 40
2x+10 = 40
2x = 30
x = 15
Problem 11 :
Company has a profit of $750 this week. This profit is $900 more than the profit P last week. Which equation can be used to find P?
a) 750 = 900 − P b) 750 = P + 900 c) 900 = P − 750 d) 900 = P + 750
Solution :
Profit for this week = $750
Let P be the profit of last week.
P + 900 = 750
So, option b is correct.
To solve for P, we have to subtract 900 on both sides.
P = 750 - 900
P = -150
Problem 12 :
The line graph shows the scoring while you and your friend played a video game. Write and solve an equation to find your score after Level 4.
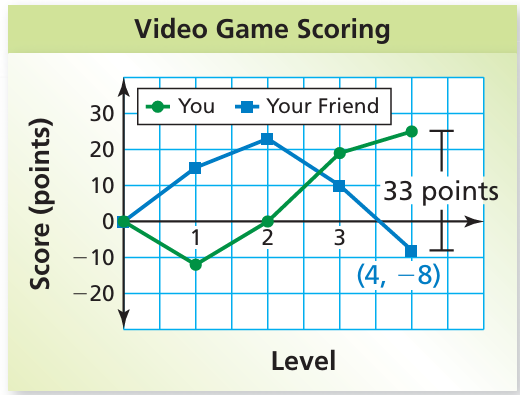
Solution :
You can determine the following from the graph.
Words Your friend’s score is 33 points less than your score.
Variable Let s be your score after Level 4.
Equation −8 = s − 33
s = -8 + 33
s = 25
Your score after Level 4 is 25 points.
Problem 13 :
The temperature of dry ice is −109.3°F. This is 184.9°F less than the outside temperature. What is the outside temperature?
Solution :
Let outside temperature be T
T - 184.9° = -109.3°
T = -109.3°+ 184.9°
T = 75.6°F
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling