WRITING A TRANSFORMED QUADRATIC FUNCTION WITH GIVEN TRANSFORMATIONS

The lowest point on a parabola that opens up or the highest point on a parabola that opens down is the vertex. The vertex form of a quadratic function is

f(x) = a(x − h)² + k

where a ≠ 0 and the vertex is (h, k).

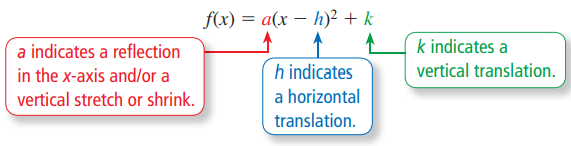
• If h > 0, move the curve h units right.
• If h < 0, move the curve h units left.
• If k > 0, move the curve h units up.
• If k < 0, move the curve h units down.

Horizontal Stretches and Shrinks f(x) = x² f(ax) = (ax)²

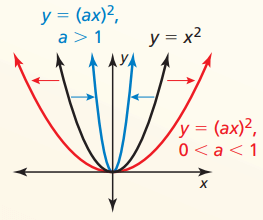
• horizontal stretch (away from y-axis) when 0 < a < 1
• horizontal shrink (toward y-axis) when a > 1

Vertical Stretches and Shrinks f(x) = x² a ⋅f(x) = ax²

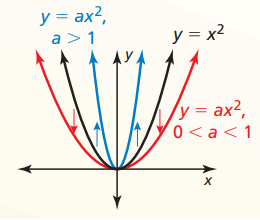
• Vertical stretch (away from x-axis) when a > 1
• Vertical shrink (toward x-axis) when 0 < a < 1

Reflections in the x-Axis :

f(x) = x²

Put y = -y

−f(x) = −(x²) = −x²

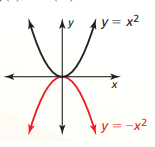
flips over the x-axis.

Reflections in the y-Axis :

f(x) = x²

Put x = -x

f(−x) = (−x)² = x²

y = x² is its own reflection in the y-axis.

Problem 1 :

f(x) = x²

vertical stretch by a factor of 2 and reflection in the x-axis followed by a translation 3 units down.

Solution :

Required transformations :

Vertical stretch -> Reflection -> Translation

So, the required transformed function is -2x² - 3.

Problem 2 :

f(x) = x²

vertical shrink by a factor of 1/2, followed by a translation 3 units left.

Solution :

Required transformations :

Vertical shrink -> Translation

f(x) = (1/2)(x -(-3))²

f(x) = (1/2)(x +3)²

So, the required transformed function is 

f(x) = (1/2)(x +3)²

Problem 3 :

f(x) = 4x² + 10

horizontal stretch by a factor of 2, followed by a translation 3 units up.

Solution :

Required transformations :

Horizontal stretch -> Translation

Replace x by (1/2)x

Problem 4 :

f(x) = (x - 2)² - 8

horizontal shrink by a factor of 1/2 and translation 5 units down, followed by a reflection in the x-axis.

Solution :

Required transformations :

Horizontal shrink -> Translation

For horizontal shrink :

Replace x by 2x

f(x) = (2x - 2)² - 8

For translation :

Replace k by k - 5

f(x) = (2x - 2)² - 8 - 5

f(x) = (2x - 2)² - 13

For reflection in x-axis :

Put y = -y

f(x) = (2x - 2)² - 13

f(x) = -[(2x - 2)² - 13]

f(x) = -(2x - 2)² + 13

So, the required function is 

f(x) = -(2x - 2)² + 13

Write a rule for g described by the transformations on the graph of f.

Problem 5 :

f(x) = x²

vertical stretch by a factor of 3 and a reflection in the x-axis by a translation 3 units down. 

Solution :

Required transformations :

Vertical stretch -> Reflection -> Translation

For horizontal shrink :

Replace x by 3x

f(x) = (3x)²

For reflection in x-axis :

Put y = -y

f(x) = -(3x)²

For translation :

Replace k by k - 3

f(x) = -(3x)² - 3

So, the required function is 

f(x) = -3x² - 3

Problem 6 :

f(x) = 4x² + 5

horizontal stretch by a factor of 2 and a translation 2 units up, followed by a reflection in the x-axis.

Solution :

Required transformations :

horizontal stretch -> Translation -> Reflection

For horizontal stretch :

Replace x by (1/2)x

For translation :

Replace k by k + 2

For reflection in x-axis :

Put y = -y

f(x) = -(x²+7)

f(x) = -x² - 7

So, the required function is f(x) = -x² - 7

Problem 7 :

Let the graph of g be a translation 4 units down and 3 units right followed by horizontal shrink by a factor of 1/2 of the graph of f(x) = x²

Solution :

Required transformations :

Translation -> Horizontal shrink

Original : f(x) = (x - 3)² - 4

After transformation: f(x) = (2x - 3)² - 4

So, the required translated function is 

f(x) = (2x - 3)² - 4

Problem 8 :

Let the graph of g be a vertical stretch by a factor of 2 and a reflection in the x-axis, followed by a translation 3 units down of the graph of f(x) = x². Write a rule for g and identify the vertex

Solution :

Original function :

f(x) = x²

For vertical stretch :

Replace x by 2x

f(x) = 2x²

For reflection in x-axis :

f(x) = -2x²

For translation :

Replace k by k - 3

f(x) = -2x² - 3

Problem 9 :

f(x) = x²; vertical stretch by a factor of 4 and a reflection in the x-axis, followed by a translation 2 units up

Solution :

Vertical stretch --> Reflection --> Translation

f(x) = x²

For vertical stretch :

f(x) = 4x²

For reflection :

f(x) = -4x²

For translation :

f(x) = -4x² + 2