WRITE THE INEQUALITY REPRESENTED BY THE GRAPH

There are four inequalities signs are used.

Less than :

For example, x < 3 means

The values of x should be lesser than 3.

Greater than :

For example, x > 3 means

The values of x should be greater than 3.

Lesser than or equal :

For example, x ≤ 3 means

The values of x should be lesser than or equal to 3.

greater than or equal :

For example, x  ≥ 3 means

The values of x should be greater than or equal to 3.

Write down the inequality which describes the region shown in each diagram.

Problem 1 :

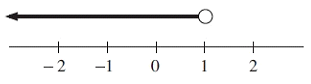
Solution :

At the top of 1, we have empty circle. So, we are allowed to use < or > sign.

What are the solutions ?

All values which are less than 1 can be considered as solution. So, the required inequality represented by the graph is

x < 1

Interval notation :

(-∞, 1)

Problem 2 :

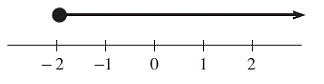
Solution :

At the top of -2, we have a solid circle. So, we are allowed to use ≤ or ≥ sign.

What are the solutions ?

All values which are greater than -2 can be considered as solution. So, the required inequality represented by the graph is

-2 ≥ x

Interval notation :

[-2, ∞)

Problem 3 :

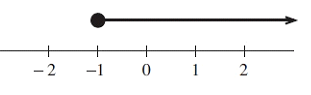
Solution :

At the top of -1, we have a solid circle. So, we are allowed to use ≤ or ≥ sign.

What are the solutions ?

All values which are greater than -1 can be considered as solution. So, the required inequality represented by the graph is

-1 ≥ x

Interval notation :

[-1, ∞)

Problem 4 :

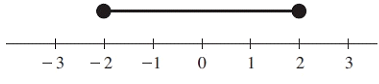
Solution :

At the top of -2 and 2, we have a solid circles. So, we are allowed to use ≤ or ≥ sign.

What are the solutions ?

All values which lies between -2 and 2 can be considered as solution. So, the required inequality represented by the graph is

-2 ≤ x ≤ 2

Interval notation :

[-2, 2]

Problem 5 :

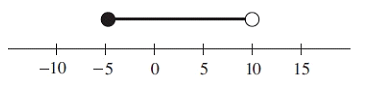
Solution :

At the top of -5, we have solid circle. At the top of 10, we have empty circle.

What are the solutions ?

All values which lies between -5 and 10 can be considered as solution. -5 is also included. So, the required inequality represented by the graph is

-5 ≤ x < 10

Interval notation :

[-5, 10]

Problem 6 :

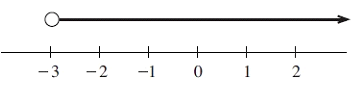
Solution :

At the top of -3, we have empty circle. At the top of -3, we have empty circle.

What are the solutions ?

All values which which are greater than -3 can be considered as solution. -5 is also excluded. So, the required inequality represented by the graph is

-3 < x < ∞

Interval notation :

(-3, ∞)

Problem 7 :

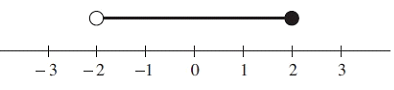
Solution :

At the top of -2, we have empty circle. At the top of 2, we have solid circle.

What are the solutions ?

All values which which are greater than -2 and lesser than 2 can be considered as solution. 

-2 < x ≤ 2

Interval notation :

(-2, 2]

Problem 8 :

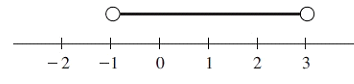
Solution :

At the top of -1 and 3, we have empty circle.

What are the solutions ?

All values which which are greater than -1 and lesser than 3 can be considered as solution. 

-1 < x < 3

Interval notation :

(-1, 3)

Problem 9 :

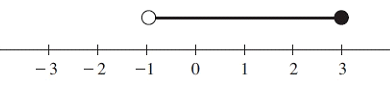
Solution :

At the top of -1, we have empty circle. At the top of 3, we have solid circle.

What are the solutions ?

All values which which are greater than -1 and lesser than 3 can be considered as solution. 3 is included and -1 is excluded.

-1 < x ≤ 3

Interval notation :

(-1, 3]

Problem 10 :

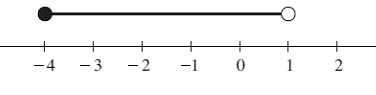
Solution :

At the top of -4, we have solid circle. At the top of 1, we have empty circle.

What are the solutions ?

All values which which are greater than -4 and lesser than 1 can be considered as solution. 

-4 ≤ x < 1

Interval notation :

[-4, 1)