WRITE LINEAR FUNCTION F WITH THE GIVEN VALUES

Problem 1 :

Write a linear function f for which f(1) = 3 and f(4) = 0

Solution :

f(1) = 3 and f(4) = 0

(1, 3) and (4, 0)

Slope = (0 - 3) / (4 - 1)

= -3/3

= -1

Equation of the line :

(y - y₁) = m (x - x₁)

(y - 3) = -1 (x - 1)

y - 3 = -x + 1

y = -x + 1 + 3

y = -x + 4

Problem 2 :

f(1) = 4 and f(0) = 6

Solution :

Converting the given inputs and outputs as set of ordered pairs.

(1, 4) and (0, 6)

Slope = (6 - 4) / (0 - 1)

= 2 / (-1)

= -2

Equation of linear function :

(y - 4) = -2(x - 1)

y - 4 = -2x + 2

y = -2x + 2 + 4

y = -2x + 6

Problem 3 :

f(1/2) = -6 and f(4) = -3

Solution :

Converting the given input and output as ordered pairs.

(1/2, -6) and (4, -3)

Slope = (-3 + 6)/(4 - 1/2)

= 3/(7/2)

= 6/7

Equation of linear function :

(y - (-3)) = (6/7)(x - 4)

(y + 3) = 6/7(x - 4)

7(y + 3) = 6(x - 4)

7y + 21 = 6x - 24

7y = 6x - 24 - 21

7y = 6x - 45

Problem 3 :

f(2/3) = -15/2 and f(-4) = -11

Solution :

Converting the given input and output as ordered pairs.

(2/3, -15/2) and (-4, -11)

Problem 4 :

A school district purchases a high-volume printer, copier, and scanner for $25,000. After 10 years, the equipment will have to be replaced. Its value at that time is expected to be $2000. Write a linear equation giving the value of the equipment during the 10 years it will be in use

Solution :

Let t be the time in years and p be the value of the product.

When the product is purchased (0, 25000)

After 10 years (10, 2000)

Slope = (25000 - 2000) / (0 - 10)

= -23000/10

= -2300

Rate of change = -2300

p = -2300t + 25000

Problem 5 :

Match the description of the situation with its graph. Also determine the slope and y-intercept of each graph and interpret the slope and y-intercept in the context of the situation. [The graphs are labeled (a), (b), (c), and (d).]

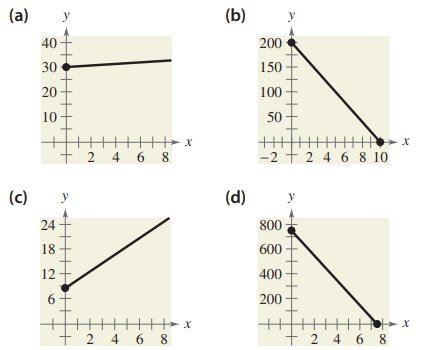
1)  A person is paying $20 per week to a friend to repay a $200 loan.

2). An employee is paid $8.50 per hour plus $2 for each unit produced per hour.

3) A sales representative receives $30 per day for food plus $0.32 for each mile traveled.

4). A computer that was purchased for $750 depreciates $100 per year

Solution :

Problem 1 :

Every week a person pays $20. The total loan amount to be paid is 200. It must be a decreasing line with the initial value 200 and slope as 20. So, graph b is correct.

Problem 2 :

Initial value = 8.50, every hour he gets 2. Then the linear function will be y = 2x + 8.50.

So, option c is correct.

Problem 3 :

The initial value = 30

Rate of change = 0.32

Let x be the number of miles traveled.

The required linear function will be y = 0.32x + 30. So, option a is correct.

Problem 4 :

The initial value of the computer is 750, it depreciates 100 per year. Let x be the number of years

y = 750 - 100 x

So, option d is correct.

Problem 6 :

The Pennsylvania State University had enrollments of 40,571 students in 2000 and 41,289 students in 2004 at its main campus in University Park, Pennsylvania. (Source: Penn State Fact Book)

(a) Assuming the enrollment growth is linear, find a linear model that gives the enrollment in terms of the year where corresponds to 2000.

(b) Use your model from part (a) to predict the enrollments in 2008 and 2010.

(c) What is the slope of your model? Explain its meaning in the context of the situation.

Solution :

Number of students enrolled initially = 40571

Rate of change :

(2000, 40571) (2004, 41289)

m = (41289 - 40571) / (2004 - 2000)

= 718 / 4

= 179.5

a) linear function will be in the form y = mx + b

Here m is rate of change, b - y-intercept or initial value

y = 179.5x + 40571

b)  Number of enrollments at 2008

When x = 8

y = 179.5(8) + 40571

y = 1436 + 40571

y = 42007

Number of enrollments at 2010

When x = 10

y = 179.5(10) + 40571

y = 1795 + 40571

y = 42366

c) Slope of the model is 179.5