WRITE EQUATIONS OF PARABOLAS IN VERTEX FORM FROM GRAPHS

Write the equation of the parabola in vertex form.

Problem 1 :

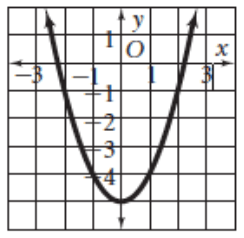
Solution :

The parabola opens up. The minimum point is at (0, -5).

Vertex (h, k) ==> (0, -5)

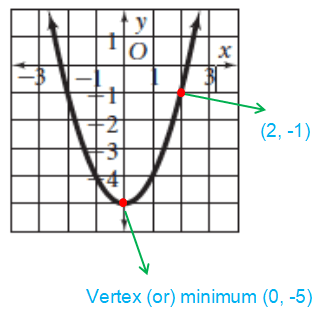
Equation of parabola :

y = a(x - h)² + k

y = a(x - 0)² + (-5) ----(1)

By observing the graph, the parabola passes through the point (2, -1).

-1 = a(2 - 0)² + (-5)

-1 = 4a + (-5)

-1 + 5 = 4a

4a = 4

a = 4/4

a = 1

By applying the value of a in (1), we get

y = 1(x - 0)² + (-5)

y = x² - 5

Problem 2 :

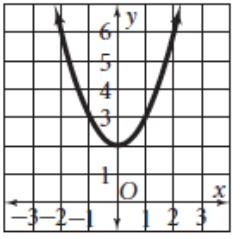
Solution :

The parabola opens up. The minimum point is at (0, 2).

Vertex (h, k) ==> (0, 2)

Equation of parabola :

y = a(x - h)² + k

y = a(x - 0)² + 2 ----(1)

By observing the graph, the parabola passes through the point (1,3).

3 = a(1 - 0)² + 2

3 = a + 2

a = 3 - 2

a = 1

By applying the value of a in (1), we get

y = 1(x - 0)² + 2

y = x² + 2

Problem 3 :

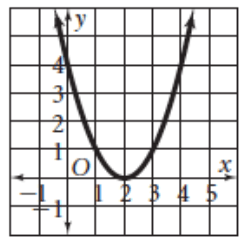
Solution :

The parabola opens up. The minimum point is at (2, 0).

Vertex (h, k) ==> (2, 0)

Equation of parabola :

y = a(x - h)² + k

y = a(x - 2)² + 0 ----(1)

By observing the graph, the parabola passes through the point (3, 1).

1 = a(3 - 2)²

1 = a(1)

a = 1

By applying the value of a in (1), we get

y = 1(x - 2)²

y = (x - 2)²

Problem 4 :

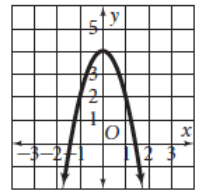
Solution :

The parabola opens up. The maximum point is at (0, 4).

Vertex (h, k) ==> (0, 4)

Equation of parabola :

y = a(x - h)² + k

y = a(x - 0)² + 4 ----(1)

By observing the graph, the parabola passes through the point (1, 2).

2 = a(2 - 0)² + 4

2 = a(4) + 4

4a = 2 - 4

4a = -2

a = -2/4

a = -1/2

By applying the value of a in (1), we get

y = (-1/2)(x - 0)² + 4

y = (-1/2)x² + 4

Problem 5 :

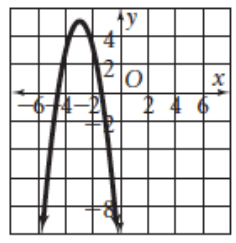
Solution :

The parabola opens up. The maximum point is at (-3, 5).

Vertex (h, k) ==> (-3, 5)

Equation of parabola :

y = a(x - h)² + k

y = a(x - (-3))² + 5

y = a(x + 3)² + 5----(1)

By observing the graph, the parabola passes through the point (-4, 2).

2 = a(-4 + 3)² + 5

2 = a(1)² + 5

a = 2 - 5

a = -3

By applying the value of a in (1), we get

y = -3(x + 3)² + 5

Problem 6 :

A parabola opens up and passes through (-4, 2) and (6, -3). How do you know that (-4, 2) is not a vertex ?

Solution :

When the given point (-4, 2) is a vertex of the parabola and it opens up, the parabola must have minimum value.

Minimum is at x = -4 and minimum value is y = 2.

By considering the other point (6, -3) the value of y is -3, it must be below the minimum. So, we decicde that (-4, 2) is not a vertex of the parabola.

Problem 7 :

A group of friends is launching water balloons. The function

f(t) = −16t² + 80t + 5

represents the height (in feet) of the first water balloon t seconds after it is launched. The height of the second water balloon t seconds after it is launched is shown in the graph. Which water balloon went higher?

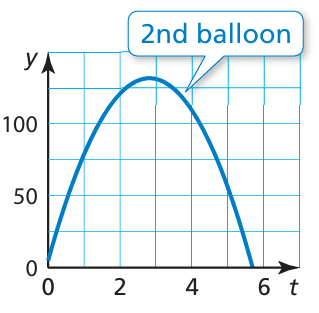
f(t) = −16t² + 80t + 5

The maximum of first water ballon :

a = -16, b = 80 and c = 5

x = -80/2(-16)

x = 80/32

x = 2.5

When x = 2.5, f(2.5) = −16(2.5)² + 80(2.5) + 5

= -16(6.25) + 200 + 5

= -100 + 205

= 105 feet

The maximum of second water ballon :

By observing the graph, the second water balloon reaches a height of about 125 feet, while the first water balloon reaches a height of only about 105 feet. So, the second water balloon went higher.

Problem 8 :

The opening of one aircraft hangar is a parabolic arch that can be modeled by the equation

y = −0.006x²+ 1.5x

where x and y are measured in feet. The opening of a second aircraft hangar is shown in the graph.

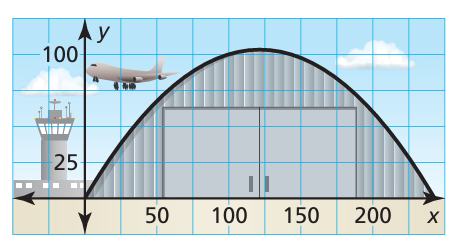
a. Which aircraft hangar is taller?

b. Which aircraft hangar is wider?

Solution :

a)  

y = −0.006x²+ 1.5x

a = -0.006, b = 1.5 and c = 0

x = -1.5/2(-0.006)

= 1.5/0.012

= 125

Applyoing x = 125, we get

y = −0.006(125)²+ 1.5(125)

= -0.006(15625) + 187.5

= -93.75 + 187.5

y = 93.75

The tallest point of the first aircraft is 93.75 ft

By observing the graph the tallest point of the second aircraft is about 120 ft

The second aircraft is taller.

b)  y = −0.006x²+ 1.5x

0 = −0.006x²+ 1.5x

1.5x(1 - 0.004 x) = 0

1.5x = 0 and 1 - 0.004 x = 0

x = 0 and x = 1/0.004

x = 0 and x = 250

Width of the first aircraft is 250 feet.

By observing the graph, the width of the second aircraft is lesser than 250 ft. So, the first aircraft is wider.