WRITE AND GRAPH A DIRECT VARIATION EQUATION WITH THE POINT
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Mathematical relationship between two variables that can be expressed by an equation in which one variable is equal to a constant times the other.
y = kx
here k is constant of variation.
The equation which is in the form y = kx is known as direct variation.
When one quantity is increased, the other quantity is also increased (or) when one quantity is decreased other quantity is also decreased.
This proportion is called direct proportion or direct variation.
When one quantity is increased, the other quantity decreased. This proportion is called inverse proportion or inverse variation.
Graphical form of direct variation will always be a straight line, may be
(i) Raising line (If constant of variation is positive)
(ii) Falling line (If constant of variation is negative).
Problem 1 :
Write and graph a direct variation equation that has a solution (3, -9).
Solution :
Direct variation equation passing through the point (3, -9)
When x = 3, y = -9
Direct variation equation y = ax
|
-9 = a(3) -9/3 = a -3 = a |
When a = -3 y = ax y = (-3)x |
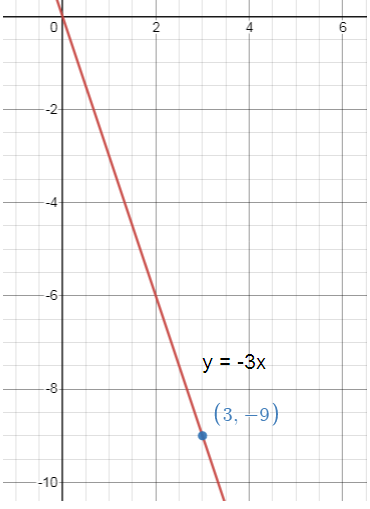
Problem 2 :
Write and graph a direct variation equation that has a solution (-7, 4).
Solution :
Direct variation equation passing through the point (-7, 4)
x = -7, y = 4
Direct variation equation y = ax
|
4 = a(-7) -4/7 = a a = -4/7 |
When a = -4/7 y = ax y = (-4x/7) |
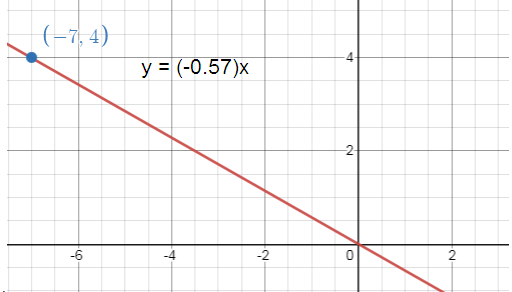
Problem 3 :
Write and graph a direct variation equation that has a solution (5, 3).
Solution :
Direct variation equation passing through the point (5, 3).
x = 5, y = 3
Direct variation equation y = ax
|
3 = a(5) 3/5 = a a = 3/5 |
y = ax When a = 3/5 y = 3x/5 |
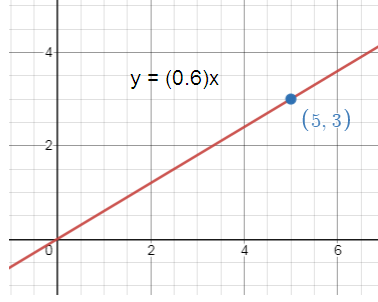
Problem 4 :
Write and graph a direct variation equation that has a solution (6, -2).
Solution :
Direct variation equation passing through the point (6, -2).
x = 6, y = -2
Direct variation equation y = ax
|
-2 = a(6) -2/6 = a a = -1/3 |
y = ax When a = -1/3 y = (-0.33)x |
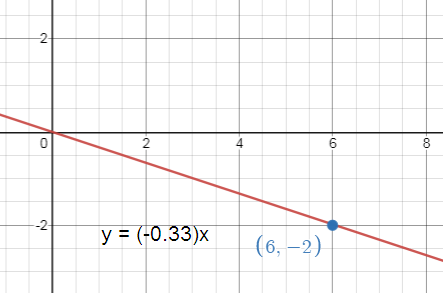
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling