WRITE A SYSTEM OF INEQUALITIES FOR THE SHADED REGION

Problem 1 :

Write the system of 2 linear inequalities graphed below.

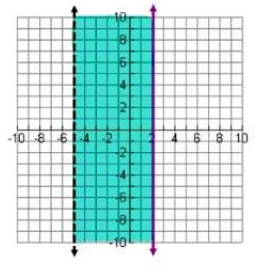
Solution:

In the above graph, we find the dotted line. So, we have to use the sign < or >.

Now, we have to look into the shaded portion. Since the shaded region is in right hand side from the dotted line, we have to use the sign ">".

x > -5

In the above graph, we find the solid line. So, we have to use the sign ≤ or ≥.

Now, we have to look into the shaded portion. Since the shaded region is in left hand side from the solid line, we have to use the sign "≤ ".

x ≤ 2

Problem 2 :

Write the system of 2 linear inequalities graphed below.

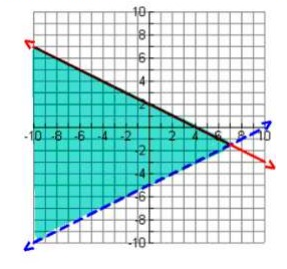
Solution:

1)

From the above graph, first let us find the slope and y-intercept.

Rise = -2 and Run = 4

Slope = -2/4 = -1/2

y-intercept = 2

So, the equation of the given line is

y = -1/2x + 2

But we need to use inequality which satisfies the shaded region.

Since the graph contains solid line, we have to use one of the signs ≤ or ≥. 

y = -1/2x + 2

Take the point (1, 1) and apply it in the equation.

1 = -1/2(1) + 2

1 = -1/2 + 2

1 = 3/2

1 = 1.5

Here 1 is less than 1.5, so we have to choose the sign ≤ instead of equal sign in the equation y = -1/2x + 2.

Hence, the required inequality is

y ≤ -1/2x + 2

2)

Rise = 5 and Run = 10

Slope = 5/10 = 1/2

y-intercept = -5

Since the graph contains dotted line, we have to use one of the signs < or >. Shaded region is above, we have to use ">".

y > 1/2x - 5

Problem 3 :

Write the system of 4 linear inequalities graphed below.

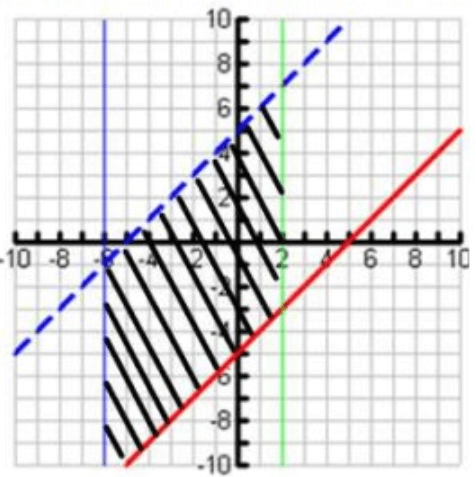
Solution:

1) Observing the graph from left to right, 

Vertical Line (blue) :

In the above graph, we find the solid line. So, we have to use the sign ≤ or ≥.

Now, we have to look into the shaded portion. Since the shaded region is in right side from the solid line, we have to use the sign " ≥".

x ≥ -6

2) Dotted line (blue) :

Rise = 5 and Run = 5

Slope = 5/5 = 1

y-intercept = 5

Since the graph contains dotted line, we have to use one of the signs < or >. Shaded region is below, we have to use "<".

y < x + 5

3) Solid line (Red) :

Rise = 5 and Run = 5

Slope = 5/5 = 1

y-intercept = -5

Since the graph contains solid line, we have to use one of the signs ≤ or ≥. Shaded region is above, we have to use "≥".

y ≥ x - 5

4) Solid line (green) :

In the above graph, we find the solid line. So, we have to use the sign ≤ or ≥.

Now, we have to look into the shaded portion. Since the shaded region is in left hand side from the solid line, we have to use the sign "≤ ".

x ≤ 2