WRITE A PIECEWISE FUNCTION FOR THE GIVEN GRAPH
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Write the function represented by the graphs given below.
Problem 1 :
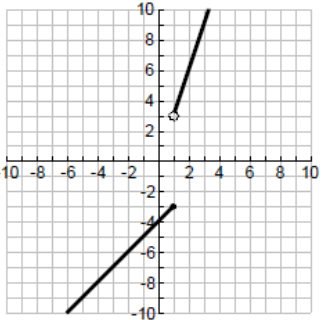
Solution :
The graph, above the x-axis is a raising line, it must be a linear function, then it must be in the form of y = mx + b
Equation of the line above x-axis :
Slope of the line = 3/1 ==> 3
y = 3x + b
Applying one of the points on the line into this equation above, we find the value of b.
(3, 9) is one of the points on the line
9 = 3(3) + b
b = 9 - 9
b = 0
So, the required function for the curve above x-axis is y = 3x.
Equation of the line below x-axis :
Slope of the line = 2/2 ==> 1
y-intercept = -4
y = x - 4
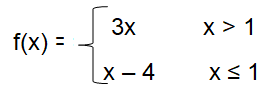
Problem 2 :
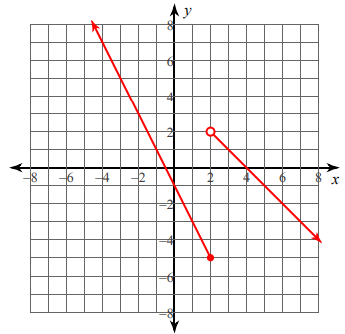
Solution :
From left to right, the first line is falling line.
Slope = -2/1 ==> -2
y-intercept = -1
y = -2x - 1
Domain for this function is x ≤ 2
From the left to right the second line is also falling line.
Slope = -1/1 ==> -1
y = -1x + b ---(1)
Applying one of the points on the line.
(4, 0)
0 = -1(4) + b
0 = -4 + b
b = 4
y = -x + 4
Domain for this function is x > 2
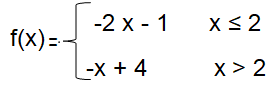
Problem 3 :
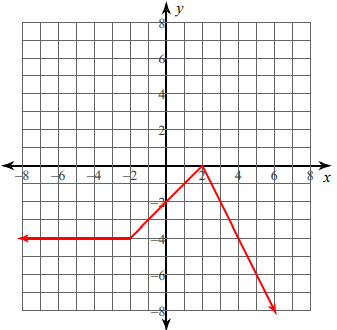
Solution :
We have three parts in the piecewise function.
1) Horizontal line
2) Raising line
3) Falling line
Equation of horizontal line :
y = -4
Domain for this function is x ≤ -2
Equation of raising line :
Slope = 1, y-intercept = -2
y = x - 2
Domain for this function is -2 < x < 2
Equation of falling line :
Slope = -2/1 => -2
y = -2x + b
Applying one of the points on the line.
The line is passing through the point (4, -4).
-4 = -2(4) + b
-4 = -8 + b
b = -4 + 8
b = 4
y = -2x + 4
Domain for this function is x ≥ 2
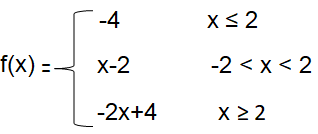
Problem 4 :
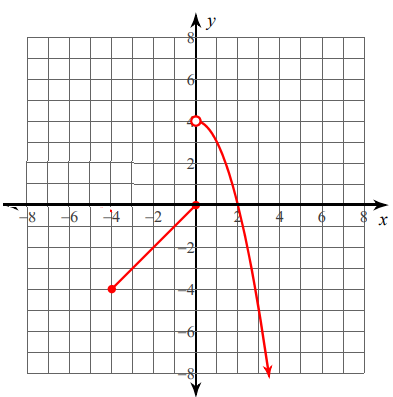
Solution :
One piece can be considered as a absolute value function.
Vertex of the absolute value function is (0,0) and it opens down.
y = a|x - h| + k
y = a|x - 0| + 0
y = a |x|
Applying one of the points on the absolute value function to figure out the value of a, we get
By applying the point (-2, -2)
-2 = a|-2|
-2 = 2a
a = -1
So, the required absolute value function is y = -|x| and its domain is -4 ≤ x ≤ 0
The other part is parabola,
y = a(x - h)2 + k
y = a(x - 0)2 + 4
y = ax 2+ 4
The curve is passing through the point (2, 0).
0 = a(2)2 + 4
4a = -4
a = -1
By applying the value of a, we get
y = -x2+ 4
It's domain is 0 < x < ∞
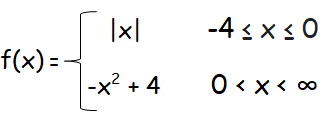
Problem 5 :
Solution :
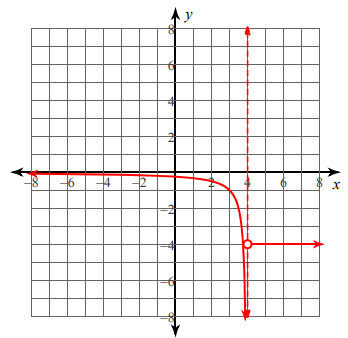
One part is the graph of reciprocal function. It's vertical asymptote is at x = 4.
Since the horizontal asymptote is x-axis o y = 0. The highest exponent of denominator is greater than the numerator.
So, the required function is f(x) = 1/(x - 4) and its domain is x ≤ 4.
Another part is horizontal line. y = -4 and its domain is 4 < x < ∞
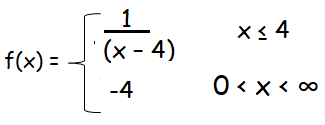
Problem 6 :
Solution :
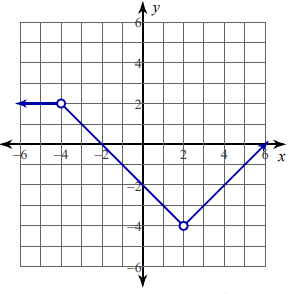
The three parts are horizontal line, falling line and raising line.
Equation of horizontal line :
y = 2 and its domain is x < -4
Equation of falling line :
Slope = -1 and y-intercept = -2
y = -x - 2 and its domain is -4 < x < 2
Equation of falling line :
Slope = 1
y = x + b
To find the value of b, applying one of the point lines on the line into the function.
The line is passing through the point (4, -2).
-2 = 4 + b
b = -6
Applying the value of b into the function, we get y = x - 6. It's domain is x > 2
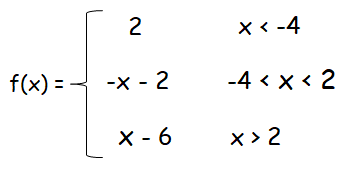
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling