WORD PROBLEMS ON VOLUME AND SURFACE AREA OF CYLINDER

A cylinder is a three dimensional solid that holds two parallel bases joined by a curved surface at a fixed distance.

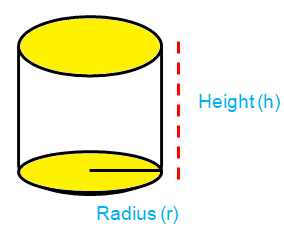
Lateral surface area of cylinder = 2πrh

Total surface area = 2πr(h + r)

Volume of cylinder = πr²h

What is surface area of cylinder ?

The surface area of a cylinder can be defined as the total space covered by the flat surfaces of the bases of the cylinder and its curved surface.

Difference between lateral and total surface area :

Lateral surface area is the area around the shape excluding top and bottom.

Total surface area is the area including top and bottom.

What is volume of cylinder ?

The volume of a cylinder is the density of the cylinder which signifies the amount of material it can carry or how much amount of any material can be immersed in it.

Problem 1 :

The radius and height of a cylinder are in the ratio 5:7 and the volume is 550 cm³. Find its total surface area.

Solution :

radius = 5x and height = 7x

Volume of cylinder = 550 cm³

Volume of cylinder = πr²h

550 = 22/7 ⋅ 5x ⋅ 5x ⋅ 7x

x³ = 550/550

x = 1

Radius = 5x = 5 × 1 = 5 cm

Height = 7x = 7 × 1 = 7 cm

Total surface area = 2πr(r + h)

= 2 × ( 22/7) ⋅ 5(5 + 7)

= 220/7 × 12

= 2640/7

= 377.14 cm²

So, total surface area of cylinder is 377.14 cm².

Problem 2 :

A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required?

Solution :

Radius = 7 m and Height = 3 m

Total surface area of the cylinder = 2πr (h + r)

= 2 ⋅ (22/7) ⋅ 7 (3 + 7)

= 44 × 10

= 440 m²

So, sheet of metal required is 440 m².

Problem 3 :     

A swimming pool is 40 m in length, 20 m in breadth and 5 m in depth. Find the cost of cementing its four walls and floor at the rate of 10 per m².

Solution :

Length = 40 m, Breadth = 20 m and Depth = 5 m

Floor area = length × breadth

Floor area = 40 × 20

= 800 m²

Area of four walls = [2 × (length + breadth)] × height

Area of four walls = [2 ⋅ (40 + 20)] × 5

= 120 × 5

= 600 m²

Total area for cementing = area of floor + area of four walls

= 800 + 600

= 1400 m²

Cost for 1 m² cementing = $10

Cost for 1400 m² cementing = (10 × 1400)

= $14000

Hence, the cost of cementing is $14000.

Problem 4 :

Two cylinders of same volume have their radii in the ratio 1:6. Find the ratio of their heights.

Solution :

Let h₁ and h₂ heights of 1^st and 2^nd cylinder respectively.

Let r₁ and r₂ radii of 1^st and 2^nd cylinder respectively.

r₁/r₂ = 1/6

r₁ = r₂/6

Volumes of both cylinders are same.

πr₁²h₁ = πr₂²h₂

Dividing by π on both sides.

r₁²h₁ = r₂²h₂

(r₂/6)²h₁ = r₂²h₂

h₁/36 = h₂

h₁/h₂ = 36/1

So, the ratio of the heights of the two cylinders is 36:1.

Problem 5 :

The curved surface area of a cylindrical pillar is 264 m² and its volume is 924 m³. The ratio of its diameter to its height is.

a) 3:7         b) 7:3        c) 6:7         d) 7:6

Solution :

Curved surface area of cylindrical pillar = 264 m²

Volume of cylindrical pillar = 924 m³

Curved surface area of cylinder = 2πrh

264 = 2πrh

264/2πr = h

132/πr = h --- > (1)

Volume of cylinder = πr²h

If r = 7 m, diameter = 2 × r = 2 × 7 = 14 m

Ratio of diameter to height = d/h

= 14/6

= 7/3

Ratio = 7:3

So, option (b) is correct.