WORD PROBLEMS ON SURFACEA AREA OF CONE

What is cone ?

A cone is a three-dimensional shape in geometry that narrows smoothly from a flat base (usually circular base) to a point(which forms an axis to the center of base) called the apex or vertex.

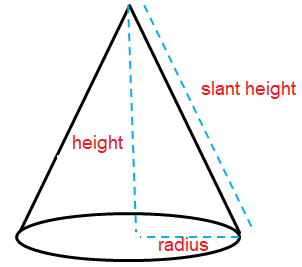
To find lateral surface area and total surface area of cone, we use the formulas given below.

Lateral surface area =  πrl

Total surface area =  πrl +  πr²

= πr(l + r)

l = √r² + h²

Here r = radius, l = slant height

Problem 1 :

Total surface area of a cone whose radius as p/2 and slant height as 2l is:

(a) 2πp(l + p)                       (b) πp(l + (p/4))

(c)  πp(l + p)                         (d) 2πpl

Solution :

Total surface area of cone = πr(l+r)

r = p/2 and l = 2l

Problem 2 :

If the slant height of a cone 12 cm and radius of the base is 14 cm, then the total surface area is.

Solution :

Slant height (l) = 12 cm, radius (r) = 14 cm

Total surface area = πr(l+r) 

Problem 3 :

The radius and height of a cone are in the ratio 4:3. The area of the base is 154 cm². Find the curved surface area

Solution :

Radius : height = 4 : 3

Radius = 4x and height = 3x

Area of the base = 154 cm²

πr² = 154

(22/7)r² = 154

r² = 154(7/22)

r² = 49

r = 7

4x = 7, then x = 7/4

height = 3(7/4) ==> 21/4 ==> 5.25

l = √7² + (5.25)²

l = √49 + 27.56

l = √76.56

l = 8.75

Curved surface area = πrl

= (22/7) . 7. (8.75)

= 192.5 cm²

Problem 4 :

There are two cones, the curved surface area of one cone is twice that of the other. The slant height of later is twice that of the former. Find the ratio of their radii.

Solution :

Curved surface area of one cone = 2 curved surface area of other

Let r₁ and l₁ be the radius and slant height of one cone

Let r₂ and l₂ be the radius and slant height of other cone

πr₁l₁= 2(πr₂l₂)  ---(1)

l₂ = 2l₁

By applying the value of L in (1), we get

πr₁l₁ = 2(πr₂(2l₁))

r₁ = 4r₂

r₁/r₂ = 4 : 1

Ratio of their radii is 4 : 1.