WORD PROBLEMS ON SETS AND VENN DIAGRAMS TWO SETS

Problem 1 :

Out of 20 members in a family, 11 like to take tea and 14 like coffee. Assume that each one likes at least one of the two drinks. How many like only tea and not coffee?

a) 9      b) 5      c) 11      d) 6

Solution :

Total number of members in the family = 20

11 - x + x + 14 - x = 20

25 - x = 20

- x = 20 - 25

-x = -5

x = 5

Number of members like tea not coffee = 11 - x

= 11 - 5

= 6

Number of members they like tea but not coffee = 6.

Problem 2 :

In a group of 20 adults, there are 8 males and 9 vegetarians. Find the number of female nonvegetarians, if the group contains 5 male vegetarians?

a) 4      b) 8       c) 12       d) 10

Solution :

Number of adults = 20

Number of males + number of females = 20

8 + number of females = 20

number of females = 20 - 8

number of females = 12

number of vegetarians = 9 out of 20

Number of non vegetarians = 11

Number of male vegetarians out of 9 vegetarian = 5

Number of female vegetarian = 9 - 5

= 4

Number female nonvegetarian = 12 - 4 ==> 8

So, the number of female non vegetarians = 8.

Problem 3 :

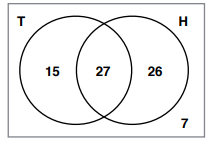
The Venn diagram alongside shows the number of people in a sporting club who play tennis (T) and hockey (H). Find the number of people:

(a) in the club        (b) who play hockey

(c) who play both sports       (d) who play neither sport

(e) who play at least one sport

(f) who play tennis but not hockey

Solution :

Number of people who play tennis only = 15

Number of people who play hockey only = 26

Number of people who play both = 27

Number of people who play none of the game = 7

a) Number of people in the club = 15 + 26 + 27 + 7

= 75

b) Number of people who play hockey = 26 + 27

= 53

(c) who play both sports = 27

(d) who play neither sport = 7

(e) who play at least one sport = 15 + 26 + 27

= 68

(f) who play tennis but not hockey = 15

Problem 4 :

In a group of 20 boys: 6 have blue eyes. 13 have fair hair. 4 have fair hair and blue eyes. 5 have neither blue eyes nor fair hair.

(a) Copy and complete the Venn Diagram with this information.

(b) How many boys have blue eyes but not fair hair?

Solution :

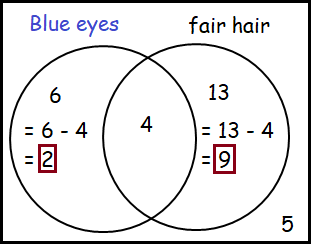
Number boys who has blue eyes but not fair hair = 2

Problem 5 :

1 In a group of 24 girls, 18 like oranges, 7 like bananas and 4 like neither oranges nor bananas.

(a) Draw a Venn diagram to illustrate this information.

(b) How many girls like both fruit?

Solution :

Let x be number of girls who like both fruit.

a)

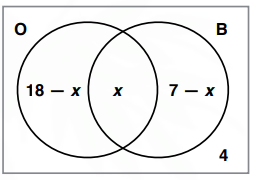
b)

Total number of girls in the group = 24

18 - x + x + 7 - x = 24

25 - x = 24

-x = 24 - 25

x = 1

So, the number of girls who like both fruit is 1.

Problem 6 :

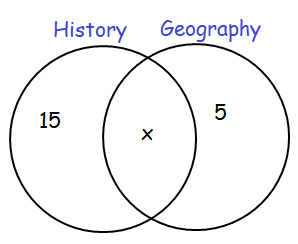
24 out of class of 32 students study History or Geography, or both. 15 study History but not Geography. 5 study Geography but not History.

(a) Draw a Venn diagram to illustrate this information.

(b) number of students who studies both History and Geography

(c) number of students who does not study History

Solution :

Total number of students = 32

Number of students who study any one subject = 24

Number of students who do not study any one of the subjects = 8

Let x be the number of students who study both.

a) 

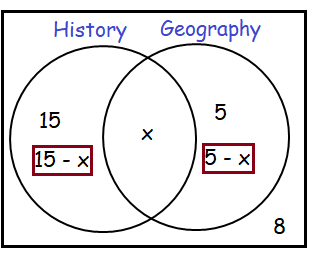
b) Number of students who study both the subject 

15 - x + x + 5 - x = 24

20 - x = 24

x = 4

c) Number of students who do not study history = 5 + 8

= 13

Problem 7 :

In a class of 30 students, 19 study Physics, 17 study Chemistry, and 15 study both of these subjects.

(a) Display this information on a Venn diagram.

(b) Find the number of students who study

(i) both subjects     (ii) at least one of the subjects

(ii) Physics but not Chemistry

(iv) exactly one of the subjects.

Solution :

a)  

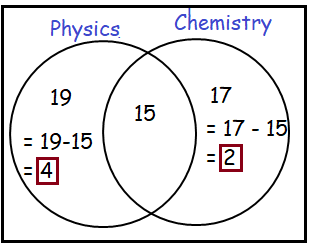
Total number of students = 30

(i) Number of students who study both subjects = 15

(ii) Number of students who study at least one of the subjects

= 4 + 15 + 2

= 22

(ii) Number of students who study Physics but not Chemistry

= 4

(iv) Number of students who study exactly one of the subjects

= 4 + 2

= 6