WORD PROBLEMS ON SEQUENCES AND SERIES

Problem 1 :

An auditorium has 20 seats on the first row, 24 seats on the second row, 28 seats on the third row, and so on and has 30 rows of seats. How many seats are in the theatre?

Solution:

First row = 20, second row = 24, third row = 28

So, the A.P is 20, 24, 28,...

a = 20

d = 24 - 20 = 4

n = 30

By using the formula of the sum of the first n terms of an A.P,

So, total seats in the theater = 2340.

Problem 2 :

Domestic bees make their honeycomb by starting with a single hexagonal cell, then forming ring after ring of hexagonal cells around the initial cell, as shown. The numbers of cells in successive rings form an arithmetic sequence.

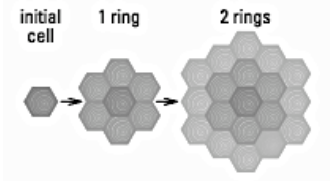
a. Write a rule for the number of cells in the nth ring.

b. What is the total number of cells in the honeycomb after the 9th ring is formed?

Solution:

a.

a_n = a + (n - 1)d

a₁ = 6

d = 6

a_n = 6 + (n - 1)6

= 6 + 6n - 6

a_n = 6n

b.

a₉ = 6(9)

a₉ = 54

S_n = n/2 (a₁ + a_n)

S₉ = 9/2 (6 + 54) 

= 9/2(60) 

S₉ = 270 

Total number of cells = 270 + 1

= 271

Problem 3 :

Suppose you go to work for a company that pays one penny on the first day, 2 cents on the second day, 4 cents on the third day and so on. If the daily wage keeps doubling, what will your total income be for working 31 days?

Solution:

a = 0.01(the decimal amount for one penny)

r = 2

n = 31

Geometric series formula for the sum of n terms,

Problem 4 :

The first year a toy manufacturer introduces a new toy, its sales total $495,000. The company expects its sales to drop 10% each succeeding year. Find the total expected sales in the first 6 years.

Solution:

The sales total is, a = 495000

The company expects its sales to drop each succeeding year, r = 1 - 10%

= 1 - 0.1

r = 0.9

Number of years n = 6

To find the total expected sales in the first 6 years,

Hence, the total expected sales in the first 6 years is $2319367.05.

Problem 5 :

The deer population in an area is increasing. This year, the population was 1.025 times last year's population of 2537.

a. Assuming that the population increases at the same rate for the next few years, write an explicit formula for the sequence where n is the number of years since the population was 2537.

b. Find the expected deer population for the tenth year.

Solution:

a.

a₁ = 2537(1.025)

a₁= 2600.425

r = 1.025

Explicit formula,

a_n = a₁(r)^n-1

a_n = 2600.425(1.025)^n-1

b.

a₁₀ = 2600.425(1.025)^10-1

= 2600.425(1.025)⁹

= 2600.425(1.2488629699)

a₁₀ = 3248

Problem 6 :

Logs are stacked in a pile with 24 logs on the bottom row and 15 on the top row. There are 10 rows in all with each row having one more log than the one above it. How many logs are in the stack?

Solution:

a₁ = 15

d = 1

n = 10

a_n = a₁ + (n - 1)d

a₁₀ = 15 + (10 - 1)1

a₁₀ = 15 + 9

a₁₀ = 24

Problem 7 :

A ball is dropped from a height of 16 feet. Each time it drops, it rebounds 80% of the height from which it is falling. Find the total distance traveled in 15 bounces.

Solution:

16, 12.8, 10.24,............

Down:

a₁ = 16

r = 0.8

n = 15

Up:

a₁ = 0.8(16) = 12.8

r = 0.8

n = 14

Total distance = 77.185 + 61.185

= 138.37 feet

So, total distance is 138.37 feet.

Problem 8 :

A company is offering a job with a salary of $30,000 for the first year and a 5% raise each year after that. If the 5% raise continues every year, find the amount of money you would earn in a 40 year career.

Solution:

a₁ = 30000

r = 1.05

n = 40