WORD PRPBLEMS ON RELATED RATES

Problem 1 :

An airplane is flying towards a radar station at a constant height of 6 km above the ground. If the distance s between the airplane and the radar station is decreasing at a rate of 400 km per hour when s = 10 km, what is the horizontal speed of the plane ?

Solution :

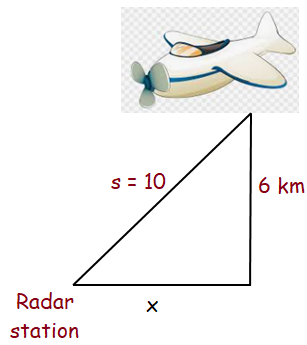
Using Pythagorean theorem :

Distance between airplane and radar station = s

Horizontal distance = x, height of airplane = 6 km

x² + 6² = s² -----(1)

x² + 6² = 10²

x² + 6² = 10²

x² = 100 - 36

x² = 64

x = 8

Differentiating (1) with respect to t, we get

Problem 2 :

A light is on the ground 20 m from building. A man 2 m tall walks from the light directly toward the building at 1 m/s. How fast is the length of his shadow on the building changing when he is 14 m from the building ?

Solution :

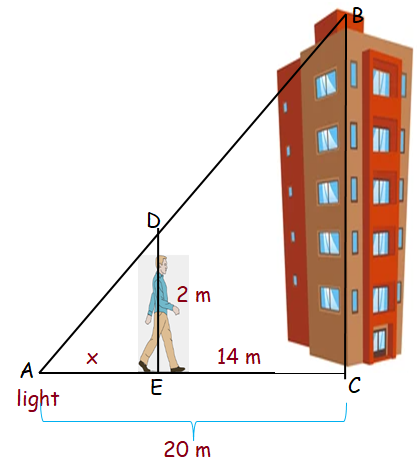
Let height of the building (BC) = h

In the picture above, we see two right triangles and they are similar.

2/h = x/20

xh = 40 ---(1)

When x = 6

h = 40/6

h = 20/3

Here x will change while the man is walking towards the building.

differentiating with respect to "t"

x(dh/dt) + h (dx/dt) = 0

dx/dt = 1 m/s, h = 20/3 and x = 6

6(dh/dt) + (20/3) (1) = 0

dh/dt = (-20/3) /  6

dh/dt = -10/9 m/s

Problem 3 :

A conical cup is 4 cm across and 6 cm deep. Water leaks out of the bottom at the rate of 2 cm³/sec. How fast is the water dropping when the height of the water is 3 cm?

Solution :

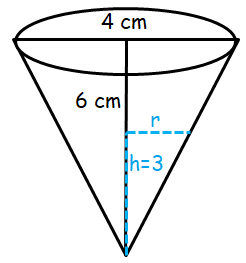
Let R be radius of conical cup and H be the height.

After the leakage r be the radius and h be the height.

While leakage happened, there will be a change in quantity of water in the cup.

V = (1/3)π r²h ----(1)

R = 2, H = 6, r = ? when h = 3

R/H = r/h

2/6 = r/3

r = 6/6

r = 1

r : h = 1 : 3

r/h =1/3

r = h/3

Applying the value of r in (1) to make the function only in terms of h, we get

V = (1/3)π (h/3)²h 

V = (1/3)π (h³/9) 

V = (h³/27)π

Differentiating with respect to "t", we get

dV/dt = (3h²π/27) dh/dt

dV/dt = (h²π/9) dh/dt

Given details :

dV/dt = -2 cm³/sec, dh/dt = ? when h = 3

-2 = (3²π/9) dh/dt

-2/π = dh/dt

dh/dt = -2/π cm/s

Problem 4 :

Air is escaping from a spherical balloon at the rate of 2 cm³ per minute. How fast is the surface area shrinking when the radius is 1 cm?

V = 4/3 πr³ and S = 4πr²

where V is the volume and S is the surface area, r is the radius.

Solution :

V = 4/3 πr³

Differentiating with respect to t, we get

dV/dt = 4/3 π(3r²) (dr/dt)

When r = 1, dV/dt = -2 cm³ per minute

-2 = (4/3) π(3(1)²) (dr/dt)

(dr/dt) = -2/4π

(dr/dt) = -1/2π

S = 4πr²

Differentiating with respect to t.

dS/dt = 4π(2r)(dr/dt)

dS/dt = 8πr (dr/dt)

When r = 1, dr/dt = -1/2π

dS/dt = 8π(1)(-1/2π)

dS/dt = -4π cm²/min

Problem 5 :

A funnel in the shape of an inverted cone is 30 cm deep and has a diameter across the top of 20 cm. Liquid is flowing out of the funnel at the rate of 12 cm³ /sec. At what rate is the height of the liquid decreasing at the instant when the liquid in the funnel is 20 cm deep?

Solution :

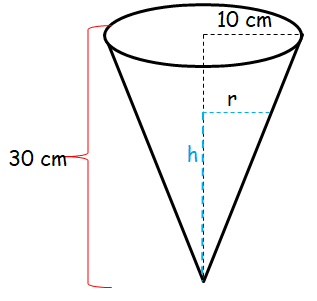
Volume of liquid in the funnel (V) = (1/3)πr² h

In the above cone, the triangles are similar.

r/h = 10/30

r = 10h/30

r = h/3

V = (1/3)π(h/3)² h

V = (1/27)πh³

dV/dt = (1/27)π(3h²) (dh/dt)

dV/dt = 12 cm³/sec, h = 20

12 = (1/9) π (20)²(dh/dt)

dh/dt = 12 (9)/400π

dh/dt = 27/100π cm/sec

Problem 6 :

Find the rate of change of the area A, of a circle with respect to its circumference C.

Solution :

Area of circle (A) = πr²

Circumference of circle (C) = 2πr

r = C/2π

A = π(C/2π)²

A = C²/4π

dA/dC = 2C/4π

dA/dC = C/2π

Problem 7 :

A boat is being pulled into a dock by attached to it and passing through a pulley on the dock, positioned 6 meters higher than the boat. If the rope is being pulled in at a rate of 3 meters/sec, how fast is the boat approaching the dock when it is 8 meters from the dock?

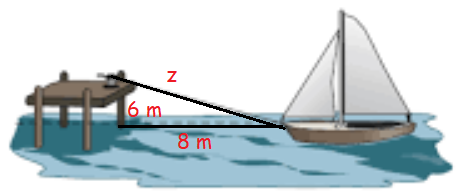
Solution :

Let x be the horizontal distance between dock and boat.

Let z be the length distance from dock and boat.

Both z and x are changing with respect to time.

x² + 6² = z² ----(1)

6² + 8² = z²

z² = 36 + 64

z² = 100

z = 10

Differentiating x² + 6² = z² ----(1) with respect to t.

2x (dx/dt) + 0 = 2z(dz/dt)

2x (dx/dt) = 2z(dz/dt)

x (dx/dt) = z (dz/dt)

x (dx/dt) = z (dz/dt)

dz/dt = -3 meters/sec, dx/dt = ?

8 (dx/dt) = 10 (-3)

dx/dt = -30/8

dx/dt = (-15/4) m/sec