WORD PROBLEMS ON LCM

Problem 1 :

There bells toll together at 10 am. The first bell tolls every 10 seconds, the second tolls every 15 seconds, and the third tolls every 20 seconds. At what time will the three bells toll together next?

Solution :

Given,

The bell will ring together at 10 am.

The 1^st bell tolls in the intervals = 10, 20, 30, .....

The 2^nd bell tolls in the interval = 15, 30, 45, ............

The 3^nd bell tolls in the interval = 20, 40, 60, ............

To find when we receive the same time on these three intervals, we find the Least Common Multiple(LCM).

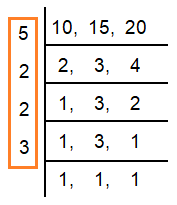
LCM of 10, 15, 20 = 5 × 2 × 2 × 3

LCM = 60 seconds

After 60 seconds three bells will ring together.

Problem 2 :

There are three tigers in a jungle. All three roar together at 6.00 am as soon as they wake up. Thereafter one roars every 20 seconds, another roars every 25 seconds and third roars every 30 seconds. When will the three tigers roar together again? When will they roar together after that?

Solution :

Given, The tigers will wake up together with a roar at 6.00 am.

The 1^st tiger is roaring in the interval = 20, 40, 60, .............

The 2^nd tiger is roaring in the interval = 25, 50, 75, ............

The 3^rd tiger is roaring in the interval = 30, 60, 90, ............

To find the three tigers roar together, we should find the least common multiple.

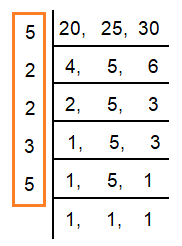
LCM of 20, 25, 30 = 5 × 2 × 2 × 3 × 5

LCM = 300 seconds

Converting seconds to minutes.

LCM = 5 minutes

After 5 minutes, the three tigers will roar together.

Problem 3 :

Water starts to drip out of two taps. A drop of water comes out of one tap every 5 seconds and out of the other tap every 7 seconds. After two drop fall together from the two taps. When will be the next time that two drops will again fall from the two taps at the same time?

Solution :

Water comes out from the 1^st and the 2^nd tap respectively in the in the following intervals.

= 5, 10, 15, 20, .............

= 7, 14, 21, 28, .............

We have to find the Least Common Multiple(LCM) of these numbers.

Here 5 and 7 are prime numbers.

LCM of 5 and 7 is 35.

So, 35 seconds water will drip out from both taps.

After 35 second water will drip out

Problem 4 :

There are three marigold plants in flower pots. A flower bloom on one plant every 2 days. The second plant bears a flower every 3 days and the third one every 4 days. If there is a flower on each of the three plants today. When will the flowers bloom together again ?

Solution :

Given,

Flowers in the 1^st and 2^nd and 3^rd plant are blooming in the following intervals

= 2, 4, 6, 8, ...............

= 3, 6,9, 12, ..................

= 4, 8, 12, ..............

To find when will the flowers bloom together again, we have to find the least common multiple.

LCM (2, 3, 4) = 12

After 12 days, the flowers on the three plants will bloom together.

Problem 5 :

In a morning walk, three persons step off together. Their steps measure 80 cm, 85 cm, and 90 cm respectively. What is the minimum distance each should walk so that all can cover the same distance in complete steps?

Solution :

Given,

Their steps measure 80 cm, 85 cm, and 90 cm respectively.

Length of the steps of 1^st person = 80, 160, 240, ...........

Length of the steps of 2^nd person = 85, 170, 255, ...........

Length of the steps of 3^rd person = 90, 180, 270, ...........

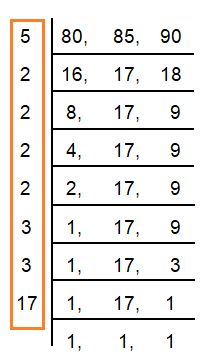
LCM of 80, 85, and 95 = 5 × 2 × 2 × 2 × 2 × 3 × 3 × 17

LCM = 12240 cm

So, the minimum distance is 12240 cm.