WORD PROBLEMS ON CONVERTING RECURSIVE AND EXPLICIT FORMS OF SEQUENCE

Problem 1 :

You have read 25 pages of a book. You plan to read an additional 10 pages each night. Write the explicit formula to represent the number of pages you will read after n nights.

Solution :

Number of paged read already = 25

Additional 10 pages to read on each night. 

The number of pages you will read after n nights.

 = 25 + 10n

Problem 2 :

In 2014, the cost to mail a letter was 49 cent for up to one ounce. Every additional ounce costs 21 cent. Which recursive function could be used to determine the cost of 3 ounce letter in cents.

(a)  a₁ = 49, a_n = a_n-1 + 21

(b)  a₁ = 21, a_n = a_n-1 + 49

(c)  a₁ = 0, a_n = 49a_n-1 + 21

(d) a₁ = 0, a_n = 21a_n-1 + 49

Solution :

a₁ = 49, a_n = a_n-1 + 21

Cost of mail a letter = 49 cent

Problem 3 :

A bicyclist is training for a race. On the first day of training, she rides 12 miles. She increases the distance she rides by 3 miles each day. Write an explicit formula to represent this scenario. How many miles will the bicyclist ride on her ninth day of training ? 

Solution :

Let x be the number of days.

and y be the miles.

The first day of training, she rides 12 miles. Each day she increases the distance of 3 miles.

Explicit formula :

a_n = a + (n – 1)d

y = 12 + (x - 1)3

= 12 + 3x – 3

y = 9 + 3x

The bicyclist ride on her ninth day of training is

y = 9 + 3(9)

y = 9 + 27

y = 36

She rides 36 miles in her ninth day.

Problem 4 :

Sofie needs to complete community service hours for her service club. She needs to complete 150 hours to earn a merit badge. Sofie has already completed 65 hours.

Write an explicit formula to represent this scenario. If she volunteers 5 hours each week, in how many weeks will she have completed the hours to earn the merit badge ?

Solution :

Let x be the number of weeks.

She needs to complete the hours = 150

Already complete the hours = 65

If she volunteers 5 hours each week.

65 + x × 5 = 150

65 + 5x = 150

5x = 150 - 65

5x = 85

x = 85/5

x = 17

After 17 weeks.

Problem 5 :

The first term of a sequence equals 5. Each term in the sequence can be obtained by subtracting 3 from twice the value of the prior term.

a) List the first four terms of the sequence.

b) Write the recursive formula for the sequence.

c) Is this an arithmetic sequence ? Explain.

Solution :

a₁ = 5

a_n  = 2a_{n - 1} - 3

a) First four terms of the sequence :

a_n = 2a_{n - 1} - 3

The first four terms of the sequence is 5, 7, 11, 19.

b) Recursive formula :

a_n = 2a_{n - 1} - 3

c) This sequence is not arithmetic progression because its common difference is not same.

Problem 6 :

The graph of an arithmetic sequence is shown to the right.

a) List the first four terms of the sequence.

b) Write the recursive formula for the sequence.

c) Find an explicit formula for the sequence.

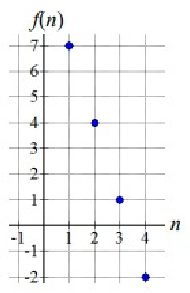
Solution :

a) First four terms of the sequence :

-2, 1, 4, 7, ....

b) Recursive formula :

a_n = a_{n - 1} + d

Common difference :

d= a₂ - a₁

= 1 - (-2)

= 1+ 2

= 3

a_n = a_n-1 + 3

c) Explicit formula :

a_n = a + (n - 1)d

a_n = -2 + (n - 1)3

= -2 + 3n - 3

= -5 + 3n