WORD PROBLEMS ON CONES AND PYRAMIDS

Find each part. All bases are regular.

Problem 1 :

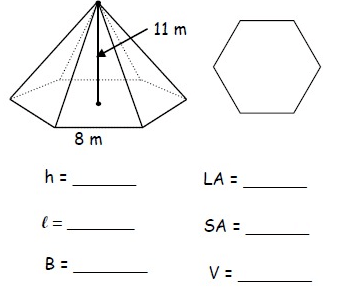
Solution :

Height (h):

Height h = 11 m

Base edge b = 8 m

Slant height (l):

Slant height l = √11² + (4√3)²

= √121 + 48

= √169

Slant height l = 13 m

Base area (B):

Perimeter = sides × base

= 6 × 8

P = 48

Base area = 1/2 × aP

= 1/2 × 4√3 × 48

Base area = 166.27 m²

Lateral area (LA):

Lateral area = 1/2 × Pl

LA = 1/2 × 48 × 13

= 24 × 13

LA = 312 m²

Surface area (SA):

Surface area = Base area + LA

SA = 166.27 + 312

SA = 478.27 m²

Volume (V):

Volume V = 1/3 × B × h

= 1/3 × 166.27 × 11

V = 609.65 m³

Problem 2 :

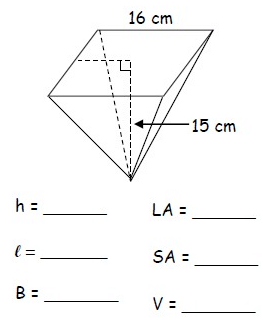
Solution :

Height (h) :

Height h = 15 cm

Base edge b = 16 cm

Slant height (l) :

Slant height = √h² + (s/2)²

= √15² + 8²

= √225 + 64

= √289

Slant height (l) = 17 cm

Base area (B) :

Base area = a²

= 16 × 16

Base area = 256 cm²

Lateral area (LA) :

Lateral area = 1/2 × Pl

LA = 1/2 × 64 × 17

LA = 544 cm²

Surface area (SA) :

Surface area = Base area + LA

= 256 + 544

 SA = 800 cm²

Volume (V) :

Volume V = 1/3 × B × h

= 1/3 × 256 × 15

V = 1280 cm³

Problem 3 :

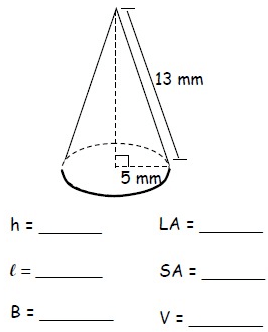
Solution :

Height (h):

Height = √l² - r²

= √13² - 5²

= √169 - 25

= √144

Height = 12 mm

Slant height (l):

Slant height = 13 mm

Base area (B):

Base area = πr²

= 3.14 × 5 × 5

B = 78.54 mm²

Lateral area (LA):

Lateral area = πrl

= 3.14 × 5 × 13

LA = 204.1 mm²

Surface area (SA):

Surface area = Base area + LA

= 78.54 + 204.1

SA = 282.64 mm²

Volume (V):

Volume V = 1/3 πr²h

= 1/3 × 3.14 × 5 × 5 × 12

V = 314 mm³

Problem 4 :

Jill made a popcorn container that is shaped like a cone. The diameter of the opening is 8 inches and the height is 9 inches. What is the volume of the popcorn container?

Solution :

Given, diameter = 8 inches

Radius = 8/2 = 4 inches

Height = 9 inches

Volume of popcorn container = 1/3 πr²h

= 1/3 × 22/7 × (4)² × 9

= 150.85 inches³

So, the volume of popcorn container is 150.85 inches³.

Problem 5 :

The lateral area of a cone is 48π in². The radius of the base is 12 in. Find the slant height.

Solution :

Given, lateral area of cone = 48π in²

Radius of the base = 12 in

Lateral area of cone = π × r × l

48π = π × r × l

48 = 12 × l

l = 48/12

l = 4 in

So, slant height of the cone is 4 in.

Problem 6 :

The volume of a square pyramid is 600 in³. The height of the pyramid is 8 in. what is the length of each base edge?

Solution :

Given, volume of square pyramid = 600 in³

Height of the pyramid = 8 in

Volume of square pyramid = 1/3 × a²h

600 = 1/3 × a² × 8

a² = 600 × 3/8

a² = 225

a = 15 in

So, length of each base edge is 15 in.

Problem 7 :

A square pyramid has a slant height of 25 m and a lateral area of 350 m². which is the closest to the volume?

a)  392 m³   b) 1176 m³   c) 404 m³   d) 1225 m³

Solution :

Given, lateral area = 350 m²

Slant height = 25 m

4 ∙ (a/2) ∙ s = 350

2a ∙ 25 = 350

50a = 350

a = 350/50

a = 7 m

The side length of the square base is 7 m.

The volume of a square pyramid = 1/3 ∙ a²h

h = √25² - (7/2)²

h = √2451/4

h = 24.75 m

V = (1/3) × 7² × 24.75

V = 404.25 m³

So, option (c) is correct.

Problem 8 :

A cereal box has the dimensions shown.

a. Find the surface area of the cereal box.

b. The manufacturer decides to decrease the size of the box by reducing each of the dimensions by 1 inch. Find the decrease in surface area.

Solution :

a) Surface area of cereal box = 2 x Area of triangles + 3 (area of rectangles)

= 2 x 1/2 x 5 x 6 + 2(6.5 x 20) + (20 x 5)

= 30 + 2(130) + 100

= 30 + 260 + 100

= 390 cm²

b) After reducing each dimension by 1 unit :

= 2 x 1/2 x 4 x 5 + 2(5.5 x 19) + (19 x 4)

= 20 + 2(104.5) + 76

= 20 + 209 + 76

= 305 cm²