WORD PROBLEMS ON AREA OF TRIANGLE TRAPEZIUM AND PARALLELOGRAM

Problem 1 :

A parking lot is constructed in the shape of a parallelogram. What is the area of the parking lot?

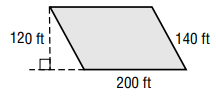
Solution :

Area of parallelogram = Base x height

Base = 200 ft and height = 120 ft

Area of parallelogram = 200 x 120

= 24000 square ft

Problem 2 :

For a school dance, a section of the gymnasium has been designated as the dance floor. Ms. Picciuto needs to determine the area of the dance floor so she will know how many students can dance at one time. What is the area of the dance floor?

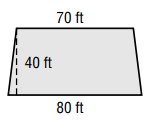
Solution :

The given shape is in the form of trapezium.

Area of trapezium = (1/2) x h x (a + b)

a = 80 ft, b = 70 ft and h = 40 ft

= (1/2) x 40 (80 + 70)

= 20(150)

= 3000 square ft

Problem 3 :

The triangular swimming pool shown is surrounded by a concrete patio. Find the area of the patio. Round to the nearest tenth if necessary.

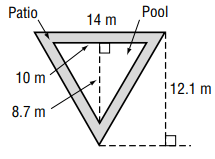
Solution :

Area of Patio = Area of large triangle - Area of small triangle

Measures of large triangle :

Base = 14 m, height = 12 m

Measures of small triangle :

Base = 10 m, height = 8.7 m

Area of shaded region = (1/2) [14 x 12 - 10 x 8.7]

= (1/2)[168 - 87]

= (1/2) x 81

= 40.5 m²

Problem 4 :

Sherice plays the bass in a garage band. Sherice’s parents let her and her friends use a section of their garage in the shape of a parallelogram for rehearsals. How much space in square feet does Sherice’s band have to practice in?

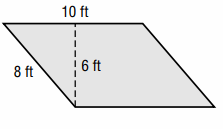
Solution :

Area of parallelogram = base x height

base = 10 ft and height = 6 ft

= 10 x 6

= 60 square ft

Problem 5 :

A 7-foot by 3-foot doorway is to be cut into the trapezoid shaped wall shown. What is the area of the wall, without the doorway?

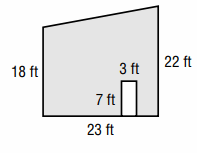
Solution :

Area of the wall without door way = area of trapezium - area of rectangle

= (1/2) x h (a + b) - length x width

= (1/2) x 23 (18 + 22) - 7 x 3

= (1/2) x 23 x 40 - 21

= 20 x 23 - 21

= 460 - 21

= 439 square ft

Problem 6 :

The wall in problem 5 is to be painted. If one can of paint covers 110 square feet, how many cans of paint will be needed if only one coat of paint is applied?

Solution :

If one can of paint covers 110 square feet.

Number of cans required = Total area to be covered / area covered by 1 can

Approximate area is 440 square feet

= 440/110

= 4 cans

4 cans are required.

Problem 7 :

Find the missing measurements for the parallelogram.

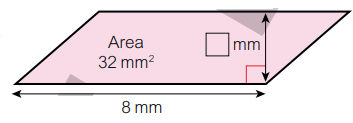
Solution :

Area of the parallelogram = 32 mm²

height = x mm, base = 8 mm

Base ⋅ height = 32

8 ⋅ x = 32

x = 32/8

x = 4 mm

Problem 8 :

Find the area of compound shape

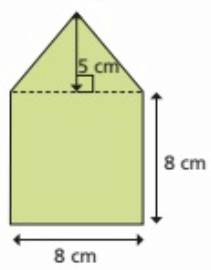
Solution :

Area of compound figure = Area of square + area of triangle

= 8² + (1/2) x 8 x 5

= 64 + 20

= 84 cm²

Problem 9 :

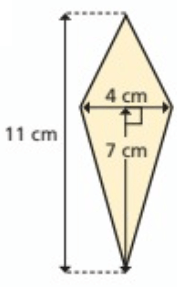
Solution :

Area of compound figure = Area of triangle above + area of triangle below

= (1/2) x 4 x 7 + (1/2) x 4 x 4

= 2 x 7 + (1/2) x 16

= 14 + 8

= 22 cm²

Problem 10 :

Kasia wants someone to paint the side of her house. It looks like below.

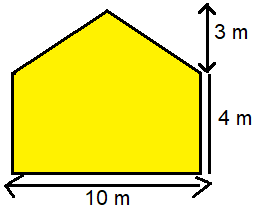
a) What is the area of the side of the house ?

b) Danilo charges $4.50 per square meter for painting. How much will Danilo charge for painting the side of the house ?

Solution :

Area to be painted = Area of triangle at the top + area of rectangle below

Measures of triangle :

base = 10 m, height = 3 m 

Area of triangle = (1/2) x base x height

= (1/2) x 10 x 3

= 15 square meter

Measures of rectangle :

length = 10 m and width = 4 m

Area of rectangle = 10 x 4

= 40 square meter

Area of the figure above = 15 + 40

= 55 square meter

Charges for painting = $4.50 per square meter

the required cost = 4.50 x 55

= $247.5