WORD PROBLEMS ON AREA OF 2D SHAPES

Problem 1:

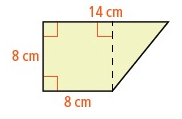
What is the area of the figure at the right?

a) 64 cm²       b) 88 cm²         c) 96 cm²        d) 112 cm²

Solution :

The figure contains a square and a right triangle.

The area of the square = 64 cm²

The area of the triangle = 1/2 × 8 × (14 - 8)

= 1/2 × 8 × 6

= 24 cm²

And 64 + 24 = 88 cm²

So, the area of the figure is 88 cm².

So, option (b) is correct.

Problem 2 :

The area of a parallelogram is 24 in², and the height is 6 in. find the length of the corresponding base.

Solution :

Area of parallelogram = 24 in²

Height = 6 in

Area of parallelogram = base × height

24 = base × 6

Base = 24/6

Base = 4 in

So, base of the parallelogram is 4 in.

Problem 3 :

A right isosceles triangle has area 98 cm². Find the length of each leg.

Solution :

A right isosceles triangle area = 98 cm²

Area of right isosceles triangle = 1/2 × a²

98 = 1/2 × a²

98 × 2 = a²

196 = a²

a = √196

a = 14 cm

So, length of each leg is 14 cm.

Problem 4 :

The area of a triangle is 108 in². A base and corresponding height are in the ratio 3 : 2. Find the length of the base and the corresponding height.

Solution :

Let the ratio be x.

Base = 3x and height = 2x

Area of triangle = 108 in²

Area of triangle = 1/2 × b × h

108 = 1/2 × b × h

108 = 1/2 × 3x × 2x

108 = 3x²

x² = 36

x = 6 in

Base = 3x = 3 × 6 = 18 in

Height = 2x = 2 × 6 = 12 in

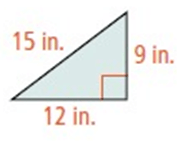
Problem 5 :

a)   Use Heron’s Formula to find the area of his triangle.

b)   Verify your answer to part (a) by using the formula

A = 1/2 bh.

Solution :   

a)

Heron’s Formula

A = √ (s × (s-a) × (s-b) × (s-c))

Where s = a + b + c / 2

s = 15 + 12 + 9 / 2

s = 36/2

s = 18

A = √ (18 × (18 - 15) × (18 - 12) × (18 - 9))

= √ (18 × 3 × 6 × 9)

= √ 2916

A = 54 in²

b)

Area of triangle = 1/2 × b × h

= 1/2 × 12 × 9

A = 54 in²

Problem 6 :

The lengths of the sides of a right triangle are 10 in, 24 in, and 26 in. what is the area of the triangle?

a.116 in²          b.120 in²        c.130 in²       d.156 in²

Solution :

Let a = 10in, b = 24 in and c = 26 in

s = (a + b + c) / 2

= (10 + 24 + 26) / 2

= 60/2

s = 30 in

Area of triangle = √(s × (s-a) × (s-b) × (s-c))

= √ (30 × (30 - 10) × (30 - 24) × (30 - 26))

= √(30 × 20 × 6 × 4)

= √14400

A = 120 in²

Problem 7 :

Find the area of a trapezoid with bases 12 cm and 18 cm and height 10 cm.

Solution :

Base 1 = 12 cm, Base 2 = 18 cm and Height = 10 cm

Area of a trapezoid = 1/2 × (base 1 + base 2) × height

= 1/2 × (12 + 18) × 10

= 1/2 × 30 × 10

A = 150 cm²

Problem 8 :

Find the area of a trapezoid with bases 2 ft and 3 ft and height 1/3 ft.

Solution :

Base 1 = 2 ft, Base 2 = 3 ft and Height = 1/3 ft

Area of a trapezoid = 1/2 × (base 1 + base 2) × height

= 1/2 × (2 + 3) × 1/3

= 1/2 × 5 × 1/3

A = 5/6 ft²

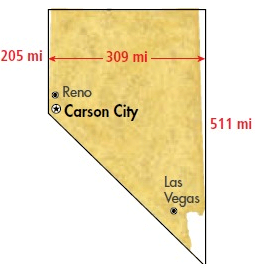
Problem 9 :

What is the approximate area of Nevada?  The area of Nevada is about 110,600 mi².

Solution :

The figure contains a rectangle and a triangle.

Given, length = 309 mi and width = 205 mi

Area of rectangle = length × width

= 309 × 205

A = 63345 mi²

Area of triangle = 1/2 × b × h

= 1/2 × 309 × (511 - 205)

= 1/2 × 309 × 306

= 309 × 153

A = 47277 mi²

And 63345 + 47277 = 110622 mi²

So, the area of Nevada is about 110,600 mi².

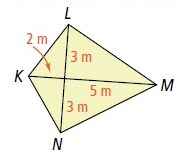
Problem 10 :

What is the area of kite KLMN?

Solution :   

Here, KM = 2 + 5 = 7m

LN = 3 + 3 = 6m

A = 1/2 × d₁ × d₂

A = 1/2 × 7 × 6

A = 21 m²

So, the area of kite KLMN is 21 m².

Problem 11 :

One base of a trapezoid is twice the other. The height is the average of the two bases. The area is 324 cm². Find the height and the lengths of the bases.

Solution :

Let, base1 = 2x and base 2 = 4x

Height = 6x/2 = 3x

Area of trapezoid = 324 cm²

Area of trapezoid = 1/2 (a + b) × h

324 = 1/2 (2x + 4x) × 3x

324 = 1/2 × 6x × 3x

324 = 9x²

x² = 324/9

x² = 36

x = 6

base1 = 2x = 2 × 6 = 12 cm

base2 = 4x = 4 × 6 = 24 cm

Height = 3x = 3 × 6 = 18 cm