WORD PROBLEMS ON AREA AND CIRCUMFERENCE OF A CIRCLE 

Problem 1 :

A circle has a radius of 6 cm. A square has a side of length 12 cm.

Work out the difference between the area of the circle and the area of the square. Give your answer correct to one decimal place

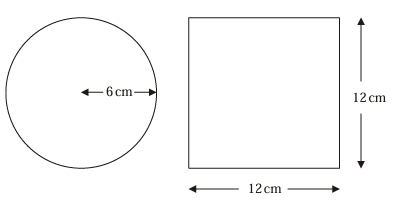
Solution :

Area of the circle = πr²

Here r = 6 cm

= π(6)²

= 36(3.14)

= 113.04 cm²

Area of square = a²

Here a = 12 cm

= 12²

= 144 cm²

Difference between the area = 144 - 113.04

= 30.96 cm²

Problem 2 :

The top of a table is a circle. The radius of the top of the table is 50 cm.

(a) Work out the area of the top of the table. The base of the table is a circle. The diameter of the base of the table is 40 cm.

(b) ………………………cm

Work out the circumference of the base of the table.

Solution :

a)  Radius of the top = 50 cm

Area of the top of the table = πr²

= (3.14) (50)²

= 7850 cm²

Area of the top of the table is 7850 cm².

b)  Diameter of the base = 40 cm

radius = 20 cm

Circumference of the base = 2πr

= 2(3.14) (20)

= 125.6 cm

Problem 3 :

The diagram shows two small circles inside a large circle. The large circle has a radius of 8 cm. Each of the two small circles has a diameter of 4 cm.

(a) Write down the radius of each of the small circles.

(b) Work out the area of the region shown shaded in the diagram. Give your answer correct to one decimal place. 

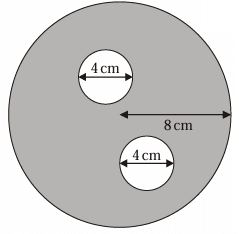
Solution :

(a) Radius of small circle = 4/2

= 2 cm

Radius of small circles are 2 cm.

(b)  Area of the shaded region

= Area of large circle - 2(area of small circles)

Area of circle = πr²

= π (8² - 2(2)²)

= π (64 - 2(4))

= π(62 - 8)

= 54π

= 54(3.14)

= 169.6 cm².

Problem 4 :

If the area of the circle is 154 cm². Its perimeter is :

Solution :

Area of the circle = 154 cm²

πr² = 154

r² = 154/(22/7)

r² = 154 (7/22)

r² = 7 x 7

r = 7 cm

Perimeter or circumference of the circle = 2πr

= 2(π)(7)

= 14 π cm

Problem 5 :

The radius of the circle whose area is equal to sum of areas of the two circles of radii 24 cm and 7 cm is ________

Solution :

Let r₁ and r₂ be the radii of two circles.

r₁ = 24 cm and r₂ = 7 cm

Sum of areas of two circles which are having the about radii.

= πr₁² + πr₂²

= π(24² + 7²)

= π(576 + 49)

= 625 π cm²

Area of the required circle = 625 π cm²

π R² = 625 π

R² = 625

R = 25

So, radius of the large circle is 25 cm.

Problem 6 :

What is the area of quadrant of a circle whose radius is 14 cm?

Solution :

A quadrant is one fourth of the circle.

Area of circle whose radius is 14 cm = π (14)²

= (22/7) x 14 x 14

= 22 x 2 x 14

= 616 cm²

Problem 7 :

What is the radius of a circle if its perimeter and area are numerically equal.

Solution :

Perimeter of the circle = area of the circle

2πr = πr²

Dividing by πr on both sides

2 = r

So, the radius of the circle is 2 cm.

Problem 8 :

The length of a minute hand of a clock is 14 cm. find the area swept by the minute hand in 5 minutes.

Solution :

Angle measure to create a circle = 360 degree 

Angle created in every 5 minutes = 360/12

= 30

Here we have to find area of the sector which is creating 30 degree angle measure.

Area of sector = (θ/360)  x πr²

= (30/360) x π(14)²

= 51.28 cm²

Problem 9 :

Find the area of quadrant of a circle whose circumference is 22 cm.

Solution :

Circumference of the quadrant = 22 cm

πr/2 + 2r = 22

r(π/2 + 2) = 22

r(22/14 + 2) = 22

r[(22 + 28) / 14] = 22

r(50/14) = 22

r = 22(14/50)

r = 6.16 cm

Problem 10 :

What is the ratio of area of two circles whose circumference are in ratio 3:4

Solution :

Let r₁ and r₂ be the radii of two circles.

2πr₁ :  2πr₂ = 3 : 4

r₁ :  r₂ = 3 : 4

r₁ /  r₂ = 3 / 4

r₁ = 3r₂/4

Ratio of area of two circles = πr₁²: πr₂²

= (3r₂/4)² : r₂²

= (9/16) : 1

= 9 : 16

So, the ratio between area of the circles is 9 : 16.