WORD PROBLEMS ON ANGLES OF A TRIANGLE

Problem 1 :

In the accompanying diagram of triangle BCD, triangle ABC is an equilateral triangle and AD = AB. What is the value of x, in degrees?

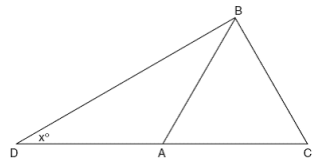
Solution :

∠BAC = ∠ACB = ∠CAB = 60°

∠BAD + ∠BAC = 180°

∠BAD + 60 = 180°

∠BAD = 180° - 60°

∠BAD = 120°

In triangle ABD, the sum of the interior angles is 180 degree.

∠ADB + ∠ABD + ∠DAB = 180°

x + x + 120 = 180°

2x = 180 - 120

2x = 60

x = 30

Problem 2 :

The measure of the vertex angle of an isosceles triangle is 15 more than the measure of each base angle. Find the  degrees in each angle of the triangle.

Solution :

Let x be the equal measure of base angle in isosceles triangle.

One vertex angle = 15 + x

Sum of the interior angles of triangle = 180

x + x + 15 + x = 180

3x + 15 = 180

3x = 180 - 15

3x = 165

x = 165/3

x = 55

Measures of base angles = 55

Measure one vertex angle = 55 + 15 ==> 70

Problem 3 :

The measure of each base angle of an isosceles triangle is seven times the measure of the vertex angle. Find the measure of each angle.

Solution :

Let x be the measure of equal angles in a isosceles triangle.

One angle = 7x

7x + x + x = 180

9x = 180

x = 180 / 9

x = 20

7x = 7(20) ==> 140

So, the angle measures are 20, 20 and 140.

Problem 4 :

The measure of each of the congruent angles of an isosceles triangle is 9 degree less than 4 times the vertex angle. Find the measure of each angle of the triangle.

Solution :

Let the vertex angle be x.

Congruent angle = 4x - 9

x + 4x - 9 + 4x - 9 = 180

9x - 18 = 180

9x = 180 + 18

9x = 198

x = 22

Problem 5 :

If

∠1 = 4x - 3y

∠2 = 3x - 5y

∠3 = 204 - 15x + 16y and ∠4 = 6x - 18

Find x and y.

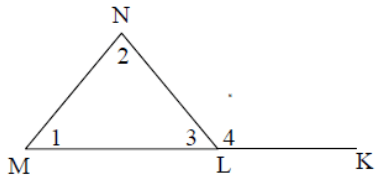
Solution :

∠1 + ∠2 + ∠3 = 4x - 3y + 3x - 5y + 204 - 15x + 16y

-8x + 8y + 204 = 180

-8x + 8y = 180 - 204

-8x + 8y = -24

Dividing by -8, we get

x - y = 3 ---(1)

∠3 + ∠4 = 180

204 - 15x + 16y + 6x - 18 = 180

-9x + 16y + 186 = 180

-9x + 16y = -6 ---(2)

(1) ⋅ 9 + (2)

9x - 9y - 9x + 16y = 27 - 6

7y = 21

y = 3

Applying the value of y in (1), we get

x - 3 = 3

x = 6

Problem 6 :

In the figure, triangle ABC is ≅ triangle FDE

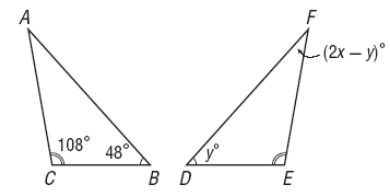
i) Find the value of x 

ii) Find the value of y.

Solution :

In triangle ABC,

∠A + ∠B + ∠C = 180

∠A + 48 + 108 = 180

∠A = 24

∠A and ∠F are congruent.

24 = 2x - y ---(1)

∠B and ∠D are congruent.

48 = y

Applying the value of y in (1), we get

24 = 2x - 48

24 + 48 = 2x

2x = 72

x = 36

Problem 7 :

In a triangle the measure of the second angle is 3 times the measure of the first angle, and the measure of the third angle is 5 times the measure of the first angle. Find the measure of each angle.

Solution :

Let x be the first angle.

second angle = 3x

third angle = 5x

Sum of interior angles = 180

 x + 3x + 5x = 180

9x = 180

x = 180/9

x = 20

Problem 8 :

In a right triangle ABC, angle A and angle B are acute angles, the measure of ∠B is 24 less than the measure of ∠A. Find ∠A and ∠B.

Solution :

∠B = ∠A - 24

Since it is right angle, one of the angle measure must be 90 degree.

∠A + ∠B = 90

∠A + ∠A - 24 = 90

2∠A = 90 + 24

2∠A = 114

∠A = 57

Then ∠B = 57 - 24

∠B = 33