WORD PROBLEMS INVOLVING POLYNOMIAL

Express the area of the figure as a polynomial in descending powers of the variable x.

Problem 1 :

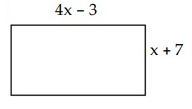
Solution :

Area of a rectangle = l × w

By observing the figure,

 l = 4x – 3, w = x + 7

Area of the rectangle = (4x – 3) (x + 7)

= 4x² + 28x – 3x -  21

= 4x² + 25x - 21

Problem 2 :

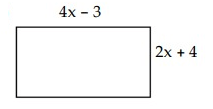
Solution :

Area of a rectangle = l × w

By observing the figure,

 l = 4x – 3, w = 2x + 4

= (4x – 3)(2x+ 4)  

= 8x² + 16x - 6x – 12

= 8x² + 10x - 12

Problem 3 :

The area of a rectangle is 20m² – 13m – 15. Find the length if the width is 4m – 5.

Solution :

Given, 20m² – 13m – 15

Length = ? and width = 4m - 5

Area of a rectangle = l × w

20m² – 13m – 15 = l × (4m – 5)

(20m² – 13m – 15)/(4m – 5) = l

(20m² – 13m – 15) = (4m – 5) (10m + 6)

 (4m – 5) (5m + 3)/ (4m – 5) = l

 5m + 3 = l

So, the length is 5m + 3.

Problem 4 :

A rectangular patio has an area of 2m³ + 12m² + 6m – 40. Find the length if the width is 2m + 8.

Solution :

Given, 2m³ + 12m² + 6m – 40

Length = ? and width = 2m + 8

Area of a rectangle = l × w

2m³ + 12m² + 6m – 40= l × (2m + 8)

(2m³ + 12m² + 6m – 40)/(2m + 8) = l

(m³ + 6m² + 3m – 20)/(m + 4) = l

Using long division method,

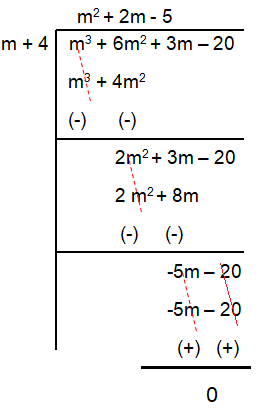
(2m³ + 12m² + 6m – 40)/(2m + 8) = m² + 2m - 5

So, the length is m² + 2m - 5.

Find simplified expressions for the perimeter and area of the given figure.

Problem 5 :

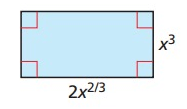
Solution :

By observing the figure,

l = 2x^2/3, w = x³

Perimeter of a rectangle = 2(l + w)

= 2(2x^2/3 + x³)

= 4x^2/3 + 2x³

Area of a rectangle = l × w

= (2x^2/3 × x³)

= 2x^{(2/3 + 3)}

= 2x^(11/3)

Problem 6 :

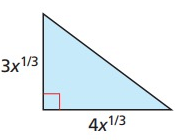
Solution :

By observing the figure,

Base (b) = 4x^1/3, height (h) = 3x^1/3

Area of triangle = 1/2 b × h

= 1/2 (4x^1/3) × (3x^1/3)

= 1/2 (12x^2/3)

= 6x^2/3

So, area of triangle is 6x^2/3.

Perimeter of right angle triangle

Using Pythagorean theorem

a² + b² = c²

a = 3x^1/3 and b = 4x^1/3

(3x^1/3)² + (4x^1/3)²  = c²

9x^2/3 + 16x^2/3 = c²

25x^2/3 = c²

c² = (5x^1/3)²

c = 5x^1/3

Perimeter of the triangle = 3x^1/3 + 4x^1/3 + 5x^1/3

= 12x^1/3

Problem 7 :

The area of a rectangular window is (2x² – 7x – 15). Both the length and the width are polynomials with integer coefficients. Which of the following could represent the length of the window? 

Solution :

Area of a rectangular window = (2x² – 7x – 15).

The length and the width are polynomials with integer coefficients.

= 2x² – 7x – 15

= 2x² – 10x + 3x – 15

= 2x(x – 5) + 3(x – 5)

= (2x+ 3) (x – 5)

So, the length of the window is 2x + 3.

Problem 8 :

A triangle is inscribed in a square, as shown. Write and simplify a function r in terms of x that represents the area of the shaded region.

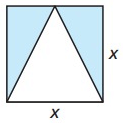
Solution :

Area of a square A = S²

= x²

Area of triangle = (1/2) b × h

= 1/2 (x²)

Area of the shaded region = area of the square  - area of the unshaded region

Area of the unshaded region is using area of the triangle.

= x² – 1/2 x²

= x²(1 – 1/2)

= x²((2 – 1)/2)

= 1/2 x²