WORD PROBLEMS EQUATIONS AND INEQUALITIES

Problem 1 :

A hybrid car gets about 60 miles per gallon of gas in the city and about 51 miles per gallon on the highway. During one week, the hybrid uses 12 gallons of gas and travels 675 miles. How much gas was used on the highway?

A) 4 gallons   B) 5 gallons   C) 7 gallons    D) 8 gallons

Solution :

Let x be the number of gallon of gas he used in highway.

Distance covered in highway + Distance covered in city = 675

60x + 51(12-x) = 675

60x + 612 - 51x = 675

9x + 612 = 675

Subtract 612 on both sides.

9x = 675 - 612

9x = 63

Divide by 9, we get

x = 63/9

x = 7

So, number of gallons used in highway is 7 gallons.

Problem 2 :

A popcorn manufacturer’s ideal weight for a bag of microwave popcorn is 3.5 ounces, with a tolerance of 0.25 ounce. What is the range of acceptable weights w (in ounces) of a bag of popcorn? 

A) w ≥ 3.75  B) w ≤ 3.25 

 C) -0.25 ≤ w ≤ 0.25  D) 3.25 ≤ w ≤ 3.75

Solution :

Weight of the popcorn bag = 3.5 ounces

Maximum weight can be added = 0.25 pounces

So, the range can be fixed as -0.25 ≤ w ≤ 0.25.

Problem 3 :

Oxygen exists as a liquid between -369°F and -297°F, inclusive. Which compound inequality gives the range of temperatures T for liquid oxygen? 

A) -369 ≤ T ≤ -297         B) -369 < T < -297

C) -297 ≤ T ≤ -369       D) -297 < T < -369

Solution :

So, the answer is  -369 ≤ T ≤ -297.

Problem 4 :

A football kicker scores 1 point for each extra point and 3 points for each field goal. One season, a kicker made 34 extra points and scored a total of 112 points. How many field goals did the kicker make?

A) 13    B) 26    C) 48   D)  78

Solution :

Let x be the number of extra field goal.

Total points = 112

34 + 3x = 112

Subtract 34 on both sides.

3x = 112 - 34

3x = 78

Divide by 3 on both sides.

x = 78/3

x = 26

Problem 5 :

A video store rents movies for $2.95 each. Recently, the store added a special allowing an unlimited number of rentals for $15.95 per month. How many movies must you rent in a month in order to save money by using the special?

A) 5 or less    B) exactly 6   C) 6 or more   D) 13 or more

Solution :

Number of rented be x.

2.95x ≤ 15.95

Divide by 2.95

x ≤ 15.95/2.95

x ≤  5.40

So, 5 or less number movies can be rented.

Problem 6 :

You are draining a swimming pool. The table shows the depth of the water at different times. How long will it take the pool to empty?

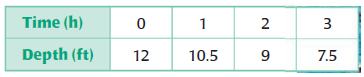
A) 4.8 hours    B) 6.7 hours   C) 8 hours    D) 24 hours

Solution :

Every hour the depth of the tank is reduced 1.5 ft.

Writing this as linear equation, y-intercept  = 12.

y = mx + b

here x represents the number if hours and y be depth of the tank.

When x = ?, y = 0

0 = -1.5x + 12

1.5x = 12

x = 12/1.5

x = 8

So, will take 8 hours to make the tank as empty.

Problem 7 :

Your parents give you $20 to help buy the new pair of shoes shown. After you buy the shoes, you have $5.50 left. Write and solve an equation to find how much money you had before your parents gave you $20.

Solution :

The starting amount + the amount your parents gave you - cost of the shoes = is the amount left

Let x be the starting amount.

x + 20 - 59.95 = 5.50

x - 39.95 = 5.50

x = 5.50 + 39.95

x = 45.45

You had $45.45 before your parents gave you money.

Problem 8 :

A bus ride costs $1.50. A 30-day bus pass costs $36. Write an inequality to represent the number of bus rides you would need to take for the bus pass to be a better deal.

Solution :

Amount spent for each ride = $1.50

Amount spent for 30 days = $36

Let x be the number of days.

1.50x > 36

x > 36/1.50

x > 24

Problem 9 :

Fifty people are seated in a movie theater. The maximum capacity of the theater is 425 people. Write an inequality to represent the number of additional people who can still be seated.

Solution :

Let x be the additional number of people.

Number of people are seated = 50

50 + x < 425

x < 425 - 50

x < 375

So, additional number of people can be seated will be lesser than 375.

Problem 10 :

A thrill ride at an amusement park holds a maximum of 12 people per ride.

a. Write and solve an inequality to find the least number of rides needed for 15,000 people.

b. Do you think it is possible for 15,000 people to ride the thrill ride in 1 day? Explain.

Solution :

a) Number of people allowed per ride = 12

Let x be the number of rides.

12 x < 15000

x < 15000/12

x < 1250

To make all 15000 to be experienced the ride, we need maximum 1250 rides.

b)  So, it is not possible to make all people to be experienced.