VERTEX AXIS OF SYMMETRY MAX MIN OF QUADRATIC FUNCTION WORKSHEET

For the questions given below, find the following.

a = ___ b = ___ c = ___

i)  Y-intercept _____

ii)  Vertex (___ , ___)

iii)  Equation of Axis of Symmetry: X = _____

iv)  Opens Up or Opens Down

v)  Maximum or Minimum

vi)  Max/Min Value _____

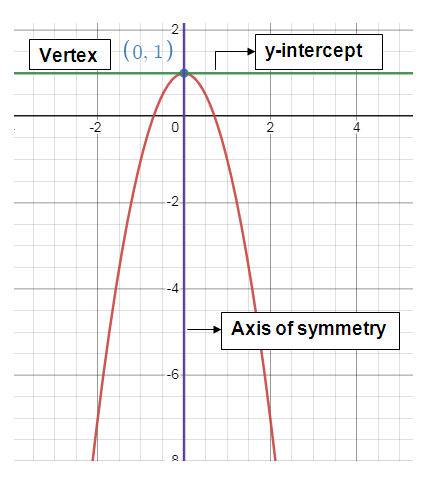
Problem 1 :

y = -2x² + 1

Solution:

y = -2x² + 1

Here a = -2, b = 0 and c = 1

y-intercept:

To find the y-intercept put x = 0.

y = -2(0)² + 1

y = 1

Vertex:

The x-coordinate of the vertex can be determined by

Substitute the value of x into the equation to find the y-coordinate of the vertex, k:

y = -2(0)² + 1

y = 1

So, the vertex is (h, k) = (0, 1).

Axis of symmetry:

Axis of symmetry of a quadratic function can be determined by the x-coordinate of the vertex.

So, the axis of symmetry is x = 0.

Opens up/Opens down:

a < 0, the parabola opens down.

Max/Min value:

The maximum value is 1.

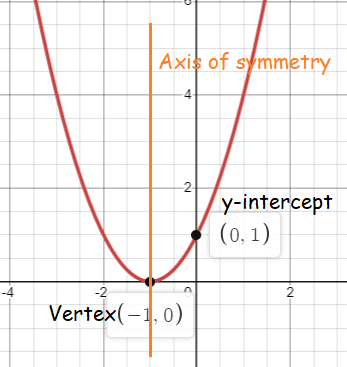
Problem 2 :

y = x² + 2x + 1

Solution:

Finding a, b and c:

a = 1, b = 2 and c = 1

y-intercept:

To find the y-intercept put x = 0.

y = (0)² + 2(0) + 1

y = 1

Vertex:

The x-coordinate of the vertex can be determined by

y = (-1)² + 2(-1) + 1

y = 1 - 2 + 1

y = 0

So, the vertex is (h, k) = (-1, 0).

Axis of symmetry:

Axis of symmetry is x = -1.

Opens up/Opens down:

a > 0, the parabola opens up.

Max/Min value:

The minimum value is 0.

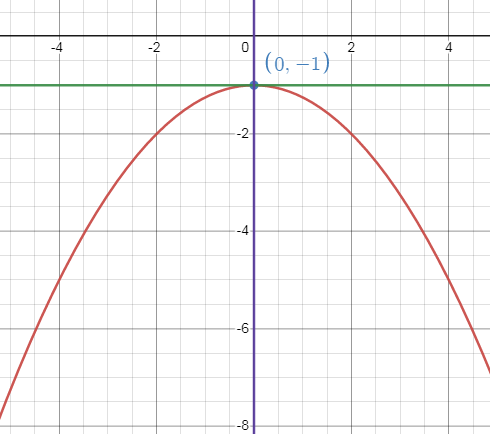
Problem 3 :

Solution:

Finding a, b and c :

a = -1/4, b = 0 and c = -1

y-intercept:

To find the y-intercept put x = 0.

y = -1/4(0)² - 1

y = -1

Vertex:

The x-coordinate of the vertex can be determined by

When x = 0

y = -1/4(0)² - 1

y = 0 - 1

y = -1

So, the vertex is (h, k) = (0, -1).

Axis of symmetry:

Axis of symmetry is x = 0.

Opens up/Opens down:

a < 0, the parabola opens down.

Max/Min value:

The maximum value is -1.

Problem 4 :

Solution:

Finding a, b and c:

a = -1/2, b = -4 and c = -1

y-intercept:

To find the y-intercept put x = 0.

y = -1/2(0)2 - 4(0) - 1

y = -1

Vertex:

The x-coordinate of the vertex can be determined by

When x = -4

y = -1/2(-4)² - 4(-4) - 1

y = -8 + 16 - 1

y = 7

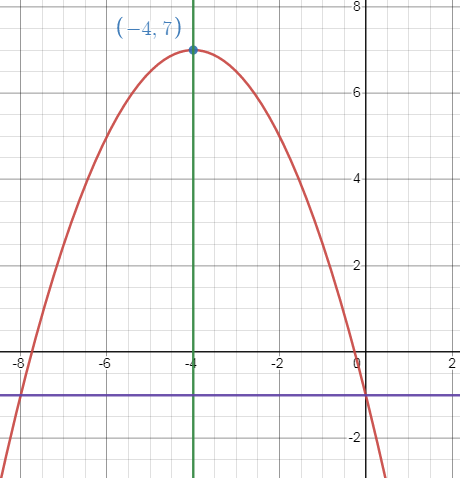
So, the vertex is (h, k) = (-4, 7).

Axis of symmetry:

Axis of symmetry is x = -4.

Opens up/Opens down:

a < 0, the parabola opens down.

Max/Min value:

The maximum value is 7.

Problem 5 :

y = 3x² - 12x - 5

Solution:

Finding a, b and c:

a = 3, b = -12 and c = -5

y-intercept:

To find the y-intercept put x = 0.

y = 3(0)² - 12(0) - 5

y = -5

Vertex:

The x-coordinate of the vertex can be determined by

When x = 2, 

y = 3(2)² - 12(2) - 5

y = 12 - 24 - 5

y = -17

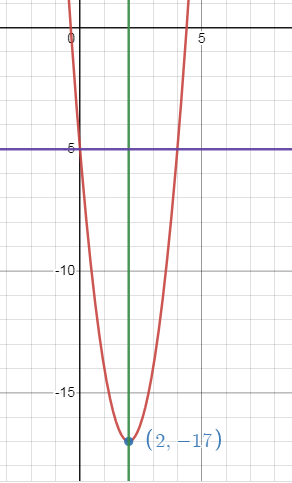
So, the vertex is (h, k) = (2, -17).

Axis of symmetry:

Axis of symmetry is x = 2.

Opens up/Opens down:

a > 0, the parabola opens up.

Max/Min value:

The minimum value is -17.

Problem 6 :

y = -x² - 8x - 13

Solution:

Finding a, b and c:

a = -1, b = -8 and c = -13

y-intercept:

To find the y-intercept put x = 0.

y = -(0)² - 8(0) - 13

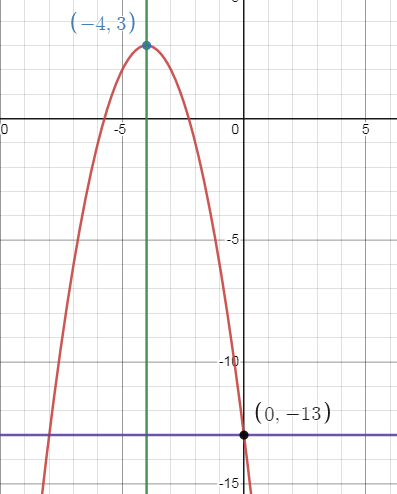
y = -13

Vertex:

The x-coordinate of the vertex can be determined by

When x = -4

y = -(-4)² - 8(-4) - 13

y = -16 + 32 - 13

y = 3

So, the vertex is (h, k) = (-4, 3).

Axis of symmetry:

Axis of symmetry is x = -4.

Opens up/Opens down:

a < 0, the parabola opens down.

Max/Min value:

The maximum value is 3.

Problem 7 :

y = x² + 2x - 2

Solution:

Finding a, b and c:

a = 1, b = 2 and c = -2

y-intercept:

To find the y-intercept put x = 0.

y = (0)² + 2(0) - 2

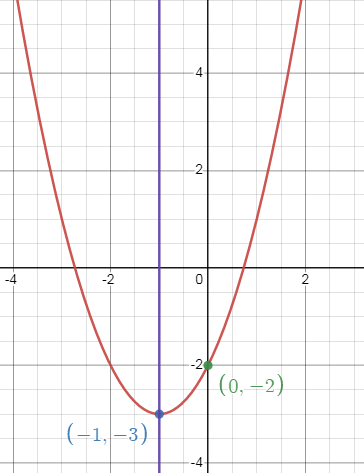
y = -2

Vertex:

The x-coordinate of the vertex can be determined by

When x = -1

y = (-1)² + 2(-1) - 2

y = 1 - 2 - 2

y = -3

So, the vertex is (h, k) = (-1, -3).

Axis of symmetry:

Axis of symmetry is x = -1.

Opens up/Opens down:

a > 0, the parabola opens up.

Max/Min value:

The minimum value is -3.

Problem 8 :

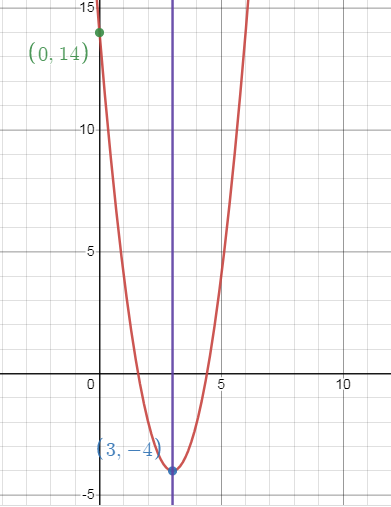
y = 2x² - 12x + 14

Solution:

Finding a, b and c:

a = 2, b = -12 and c = 14

y-intercept:

To find the y-intercept put x = 0.

y = 2(0)² - 12(0) + 14

y = 14

Vertex:

The x-coordinate of the vertex can be determined by

When x = 3

y = 2(3)² - 12(3) + 14

y = 18 - 36 + 14

y = -4

So, the vertex is (h, k) = (3, -4).

Axis of symmetry:

Axis of symmetry is x = 3.

Opens up/Opens down:

a > 0, the parabola opens up.

Max/Min value:

The minimum value is -4.