VERIFYING GEOMETRIC PROPERTIES OF TRIANGLE USING ANALYTIC GEOMETRY

Problem 1  :

The vertices of a triangle are K(2, -6), L(4, 10) and M(8, -2). Let P be the midpoint of KL and Q be the midpoint of LM. Verify that :

a) PQ is parallel to KM

b) PQ is half the length of KM.

Solution :

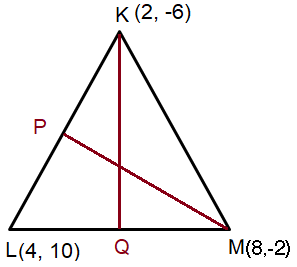
a)

Given, K(2, -6), L(4, 10) and M(8, -2)

Let P be the midpoint of KL.

Midpoint formula is 

K (2, -6) and L (4, 10)

x₁ = 2, y₁ = -6, x₂ = 4, y₂ = 10

Let  Q be the midpoint of LM.

Midpoint formula is 

L(4, 10) and M(8, -2)

x₁ = 4, y₁ = 10, x₂ = 8, y₂ = -2

Slope of a line formula :

Let P = (3, 8) and Q = (6, 4)

x₁ = 3, y₁ = 8, x₂ = 6, y₂ = 4

M(8, -2) and K(2, -6)

x₁ = 8, y₁ = -2, x₂ = 2, y₂ = -6

So, PQ is parallel to KM.

b) 

P = (3, 2) and Q = (6, 4)

x₁ = 3, y₁ = 2, x₂ = 6, y₂ = 4

PQ = √[(6 - 3)² + (4 - 2)²]

= √[3² + 2²] 

= √[9 + 4]

PQ = √13

PQ = 5

 K(2, -6) and M(8, -2)

x₁ = 2, y₁ = -6, x₂ = 8, y₂ = -2

KM = √[(8 - 2)² + (-2 + 6)²]

= √[(6)² + (4)²] 

= √[36 + 16]

KM = √52

= √(2 x  2 x 13)

= 2√13

Length of KM = 2 length of PQ

Problem 2 :

Given ∆ABC with vertices A(-7, 3), B(-2, -3) and C(4, 2).

a) Classify the triangle by side length

b) Verify that one median of the triangle is perpendicular to one of the sides.

Solution :

a) 

Given, A(-7, 3), B(-2, -3) and C(4, 2)

l = √[(x₂ - x₁)² + (y₂ - y₁)²]

A(-7, 3) and B(-2, -3)

x₁ = -7, y₁ = 3, x₂ = -2, y₂ = -3

AB = √[(-2 + 7)² + (-3 - 3)²]

= √[(5)² + (-6)²]

= √[25 + 36]

AB = √61

B(-2, -3) and C(4, 2)

x₁ = -2, y₁ = -3, x₂ = 4, y₂ = 2

BC = √[(4 + 2)² + (2 + 3)²]

= √[(6)² + (5)²]

= √[36 + 25]

BC = √61

C(4, 2) and A(-7, 3)

x₁ = 4, y₁ = 2, x₂ = -7, y₂ = 3

CA = √[(-7 - 4)² + (3 - 2)²]

= √[(-11)² + (1)²]

= √[121 + 1]

CA = √122

Since the two sides are equal, it must be a isosceles triangle. 

b)  D is the midpoint of BC.

B(-2, -3) and C(4, 2)

x₁ = -2, y₁ = -3, x₂ = 4, y₂ = 2

Midpoint = (-2+4)/2, (-3+2)/2

= D(1, -1/2)

Slope of AD :

A(-7, 3) and D(1, -1/2)

= (-1/2 - 3) / (1 + 7)

= (-7/2) / 8

= -7/16

Slope of BC :

B(-2, -3) and C(4, 2)

= (2 + 3) / (4 + 2)

= 5/6

E is the midpoint of AC.

A(-7, 3) and C(4, 2)

x₁ = -7, y₁ = 3, x₂ = 4, y₂ = 2

Midpoint = (-7+4)/2, (3+2)/2

= E(-3/2, 5/2)

Slope of BE :

B(-2, -3) and E(-3/2, 5/2)

Slope of AC :

A(-7, 3) and C(4, 2)

= (2 - 3) / (4 + 7)

= -1/11

Median BE and AC are perpendicular to each other.