USING VECTORS PROVE COMPOUND ANGLE FORMULAS

Problem 1 :

Using vector method, prove that

cos (α - β) = cos α cos β + sin α sin β

Solution :

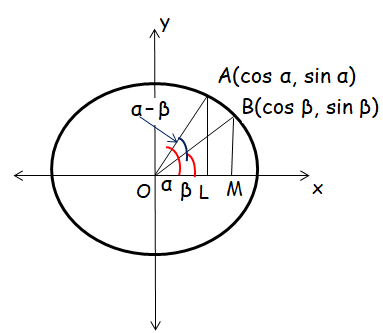
In the unit circle with center O, OA and OB are radii.

∠AOX = α, ∠BOX = β and ∠AOB = α - β

AL and AM are perpendiculars to the x-axis.

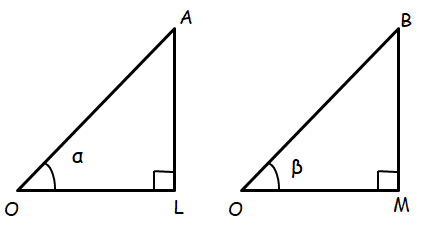
In triangle OAL,

OA = hypotenuse = 1, AL = opposite side, OL = adjacent side

A(x-coordinate, y-coordinate)

cos α = Adjacent side / hypotenuse

A(x-coordinate, y-coordinate)

This is how, A(cos α, sin α)

In triangle OBM,

OB = hypotenuse = 1, BM = opposite side, OM = adjacent side

B(x-coordinate, y-coordinate)

cos β = Adjacent side / hypotenuse

sin β = Opposite side / hypotenuse

B(x-coordinate, y-coordinate)

This is how, B(cos β, sin β)

Problem 2 :

Prove by vector method that

sin (α + β) = sin α cos β + cos α sin β

Solution :

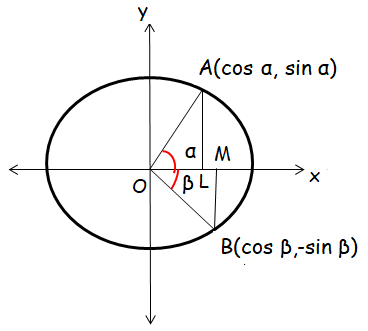
In the unit circle with center O, OA and OB are radii.

∠AOX = α, ∠BOX = β and ∠AOB = α + β

AL and AM are perpendiculars to the x-axis.

In triangle OAL,

OA = hypotenuse = 1, AL = opposite side, OL = adjacent side

A(x-coordinate, y-coordinate)

cos α = Adjacent side / hypotenuse

A(x-coordinate, y-coordinate)

This is how, A(cos α, sin α)

In triangle OBM,

OB = hypotenuse = 1, BM = opposite side, OM = adjacent side

B(x-coordinate, y-coordinate)

cos β = Adjacent side / hypotenuse

sin β = Opposite side / hypotenuse

B(x-coordinate, -y-coordinate)

This is how, B(cos β, -sin β)