USING TRIANGLE PROPORTONALITY THEOREM FIND THE MISSING LENGTH
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If a line is parallel to one side of a triangle and intersects the other two sides, then it divides the two sides proportionally.
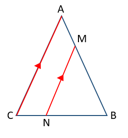
Consider the triangles NBM and CAB.
∠MNB = ∠ACB
∠NBM = ∠CBA
triangles NMB and CAB are similar, then corresponding sides will be in the same ratio.
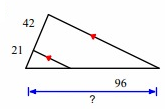
Problem 1 :
Solution :
Line segment ED is parallel to the side AC.
By Triangle Proportionality Theorem,
So, the missing length is 144.
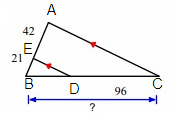
Problem 2 :
Solution :
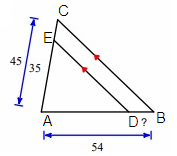
Line segment ED is parallel to the side AC.
By Triangle Proportionality Theorem,
So, the missing length is 12.
Problem 3 :
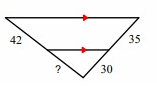
Solution :
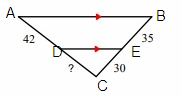
Line segment AB is parallel to the side DE.
By Triangle Proportionality Theorem,
So, the missing length is 36.
Problem 4 :
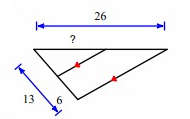
Solution :
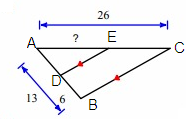
Line segment DE is parallel to the side BC.
By Triangle Proportionality Theorem,
So, the missing length is 14.
Problem 5 :
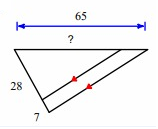
Solution :
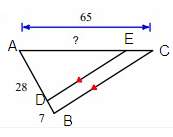
Line segment DE is parallel to the side BC.
By Triangle Proportionality Theorem,
So, the missing length is 52.
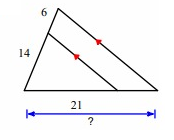
Problem 6 :
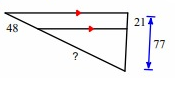
Solution :
Line segment AB is parallel to the side DE.
By Triangle Proportionality Theorem,
So, the missing length is 128.
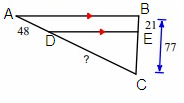
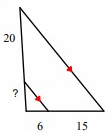
Problem 7 :
Solution :
Line segment ED is parallel to the side AC.
By Triangle Proportionality Theorem,
So, the missing length is 50.
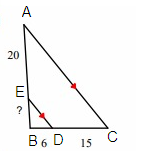
Problem 8 :
Solution :
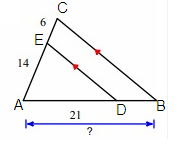
Line segment ED is parallel to the side BC.
By Triangle Proportionality Theorem,
So, the missing length is 30.
Problem 9 :
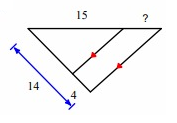
Solution :
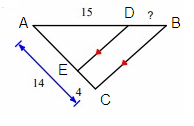
Line segment ED is parallel to the side CB.
By Triangle Proportionality Theorem,
So, the missing length is 6.
Problem 10 :
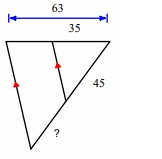
Solution :
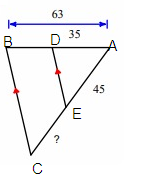
Line segment BC is parallel to the side DE.
By Triangle Proportionality Theorem,
So, the missing length is 36.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling