USING TRANSFORMATIONS TO GRAPH QUADRATIC FUNCTIONS

Translation

f(x) = a(x − h)² + k

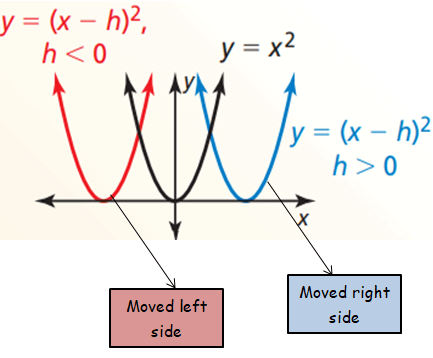
Horizontal translation :

Moving the graph towards left or right.

h > 0, then move the graph right.

h < 0, then move the graph left.

Vertical translation :

Moving the graph towards up or down.

k > 0, then move the graph up.

k < 0, then move the graph down.

Reflection

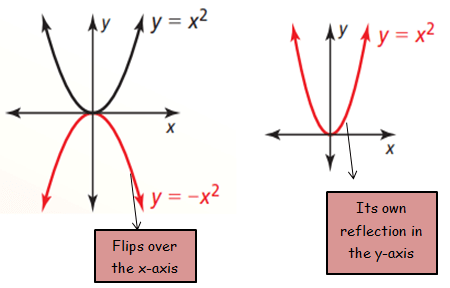
Reflection across x-axis :

f(x) = x²

-f(x) = -x²

Reflection across y-axis :

f(x) = x²

f(-x) = (-x)²

Shrinks and Stretches

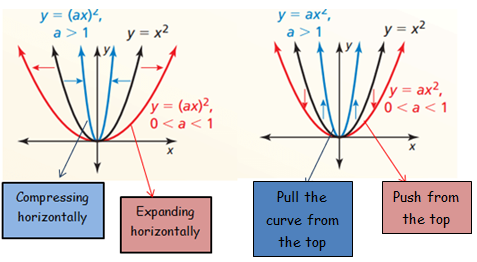
Horizontal stretches and shrinks :

f(x) = x²

f(ax) = (ax)²

If a > 1 (horizontal shrink)

If 0 < a < 1 (horizontal stretch)

Vertical stretches and shrinks :

f(x) = x²

a f(x) = ax²

If a > 1 (vertical stretch)

If 0 < a < 1 (vertical shrink)

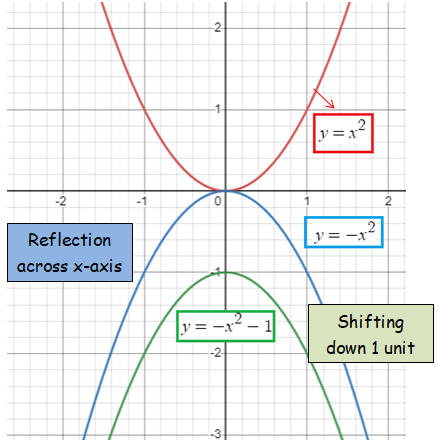
Write the equation for the function y = x² with the following transformations and draw the graph of it.

Problem 1 :

Reflect across the x-axis, shift down 1 

Solution :

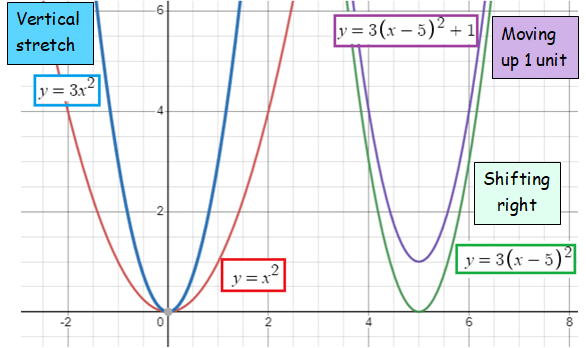
Problem 2 :

Vertically stretch by a factor of 3, shift right 5 and up 1

Solution :

Problem 3 :

If you wanted to shift

y = -3(x – 2)² + 1

down 4 and left 5 what would be the new equation?

Solution :

So, the required quadratic function is

y = -3(x + 3)² - 3

Problem 4 :

If you wanted to shift y = x² + 3 left 2 and up 5 what would be the new equation?

Solution :

So, the required quadratic function is

y = (x + 2)² + 8

Problem 5 :

If you wanted to shift y = (x + 4)² down 3 and right 2 what would be the new equation?

Solution :

So, the equation of the required quadratic function is 

y = (x + 2)² + 3

Problem 6 :

If you wanted to shift y = -x² right 3 and up 5 what would be the new equation?

Solution :

So, the required equation is 

y = (x - 3)² + 5

Problem 7 :

Describe the following transformations on the function y = x²

y = (x + 3)² -1

Solution :

y = (x + 3)² -1

y = (x - (-3))² -1

Horizontal shift of 3 units left and vertical shift of 1 unit down.

Problem 8 :

Describe the following transformations on the function y = x²

y = -(1/2)(x - 1)² + 3

Solution :

y = -(1/2)(x - 1)² + 3

Comparing with y = a(x - h)² + k

a = -1/2, h = 1 and k = 3

Reflection across x -axis, vertical compression of 1/2 units, horizontal shift of 1 unit right and vertical shift of 3 units up.

Problem 9 :

Describe the following transformations on the function y = x²

y = (1/3)(x + 2)² + 3

Solution :

y = (1/3)(x + 2)² + 3

y = (1/3)(x - (-2))² + 3

Comparing with y = a(x - h)² + k

a = 1/3, h = -2 and k = 3

Vertical compression of 1/3 units, horizontal shift of 2 units left and vertical shift of 3 units up.