USING THE CENTROID OF A TRIANGLE TO FIND SEGMENT LENGTHS

The centroid theorem states that the centroid of the triangle is at 2/3 of the distance from the vertex to the mid-point of the sides.

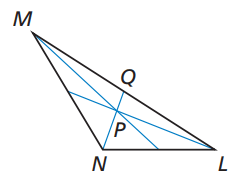
Point P is the centroid of △LMN. Find PN and QP.

Problem 1 :

Given that QN = 9

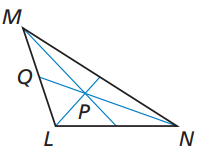
Solution :

Problem 2 :

Given that QN = 21

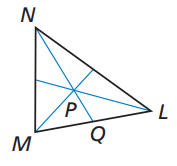
Solution :

Problem 3 :

Given that QN = 30

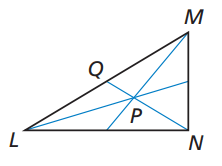
Solution :

Problem 4 :

Given that QN = 42

Solution :

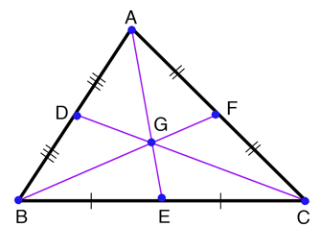
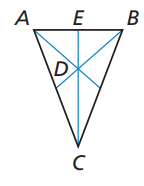
Point D is the centroid of △ABC. Find CD and CE.

Problem 5 :

Given that DE = 5, find CD and CE.

Solution :

CD = (2/3) CE

CD = (2/3) (CD + DE)

CD = (2/3) (CD + 5)

3CD = 2(CD + 5)

3CD = 2CD + 10

3CD - 2CD = 10

CD = 10

CE = CD + DE

CE = 10 + 5

CE = 15

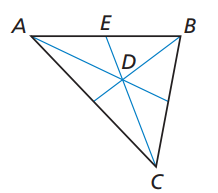
Problem 6 :

Given that DE = 11, find CD and CE.

Solution :

CD = (2/3) CE

CD = (2/3) (CD + DE)

CD = (2/3) (CD + 11)

3CD = 2(CD + 11)

3CD = 2CD + 22

3CD - 2CD = 22

CD = 22

CE = CD + DE

CE = 22 + 11

CE = 33

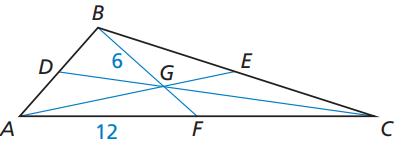
Problem 7 :

Point G is the centroid of △ABC. BG = 6, AF = 12, and AE = 15. Find the length of the segment.

i) FC    ii)  BF    iii)  AG     iv)  GE

Solution :

Definition of centroid :

The point where three medians of the triangle intersect is known as centroid.

Accordingly definition of centroid, BF should be the median of AC.

i)  AF = FC = 12

ii)  BG = (2/3) ⋅ BF 

6 = (2/3) ⋅ BF 

18/2 = BF

BF = 9

iii)  AG = (2/3) ⋅ AE

 AG = (2/3) ⋅ 15

AG = 10

iv)  AE = AG + GE

15 = 10 + GE

GE = 15 - 10

GE = 5

Point D is the centroid of △ABC. Use the given information to find the value of x.

Problem 8 :

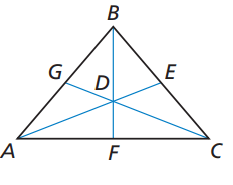
1) BD = 4x + 5 and BF = 9x

2) GD = 2x − 8 and GC = 3x + 3

3) AD = 5x and DE = 3x − 2

4) DF = 4x − 1 and BD = 6x + 4

Solution :

1) BD = 4x + 5 and BF = 9x

BD = (2/3) BF

(4x + 5) = (2/3) 9x

4x + 5 = 2(3x)

4x + 5 = 6x

6x - 4x = 5

2x = 5

x = 5/2

x = 2.5

2) GD = 2x − 8 and GC = 3x + 3

GD = (1/3) GC

2x - 8 = (1/3)(3x + 3)

2x - 8 = x + 1

2x - x = 1 + 8

x = 9

3) AD = 5x and DE = 3x − 2

AD = (2/3) AE

AE/3 = AD/2  ---(1)

DE = (1/3) AE

AE/3 = DE  ----(2)

(1) = (2)

5x/2 = 3x - 2

5x = 6x - 4

5x - 6x = -4

-x = -4

x = 4

4) DF = 4x − 1 and BD = 6x + 4

DF = (1/3) BF

DF = BF/3 -----(1)

BD = (2/3) BF

BD/2 = BF/3  -----(2)

(1) = (2)

DF = BD/2

4x - 1 = (6x + 4)/2

2(4x - 2) = 6x + 4

8x - 6x = 4 + 4

2x = 8

x = 4