USING PASCAL TRIANGLE TO EXPAND BINOMIALS

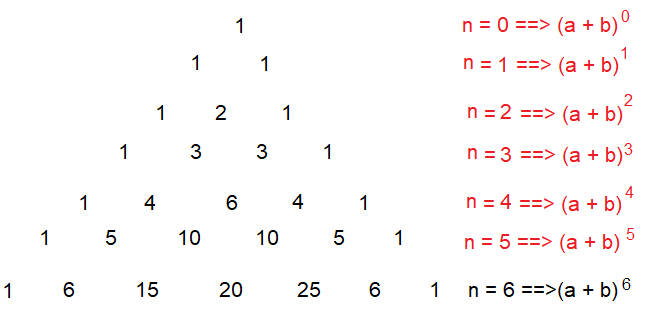
Consider the following expanded powers of (a + b)ⁿ, where a + b is any binomial and n is a whole number. Look for patterns.

Each expansion is a polynomial. There are some patterns to be noted.

1. There is one more term than the power of the exponent, n. That is, there are terms in the expansion of (a + b)ⁿ.

2. In each term, the sum of the exponents is n, the power to which the binomial is raised.

3. The exponents of a start with n, the power of the binomial, and decrease to 0. The last term has no factor of a. The first term has no factor of b, so powers of b start with 0 and increase to n.

4. The coefficients start at 1 and increase through certain values about "half"-way and then decrease through these same values back to 1.

Use the binomial expansion of (a + b)³ to expand and simplify:

Problem 1 :

(x + 1)³

Solution :

From the pascal triangle above,

(a + b)³ = a³ + 3a²b + 3ab² + b³

a = x and b = 1

(x + 1)³ = x³ + 3(x)²(1) + 3(x)(1)² + 1³

(x + 1)³ = x³ + 3x² + 3x + 1

Use (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴ to expand and simplify:

Problem 2 :

(x - 2)⁴

Solution :

Using pascal's triangle, we get

Since, we have negative in the middle, we 

(a - b)⁴ = a⁴ - 4a³b + 6a²b² - 4ab³ + b⁴

a = x and b = 2

(x - 2)⁴ = x⁴ - 4(x)³(2) + 6(x)²(2)² - 4(x)(2)³ + (2)⁴

(x - 2)⁴ = x⁴ - 8x³ + 24x² - 32x + 16

Problem 3 :

(2x + 3)⁴

Solution :

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

a = 2x and b = 3

(2x + 3)⁴ = (2x)⁴ + 4(2x)³(3) + 6(2x)²(3)² + 4(2x)(3)³ + (3)⁴

(2x + 3)⁴ = 16x⁴ + 96x³ + 216x² + 216x + 81

Problem 4 :

(x + 1/x)⁴

Solution :

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

a = x and b = 1/x

(x + 1/x)⁴ = (x)⁴ + 4(x)³(1/x) + 6(x)²(1/x)² + 4(x)(1/x)³ + (1/x)⁴

(x + 1/x)⁴ = x⁴ + 4x² + 6 + 4/x² + 1/x⁴

Problem 5 :

(2x - 1/x)⁴

Solution :

(a - b)⁴ = a⁴ - 4a³b + 6a²b² - 4ab³ + b⁴

a = 2x and b = 1/x

(2x - 1/x)⁴ = (2x)⁴ - 4(2x)³(1/x) + 6(2x)²(1/x)² - 4(2x)(1/x)³ + (1/x)⁴

(2x - 1/x)⁴ = 16x⁴ - 32x² + 24 - 8/x² + 1/x⁴

Problem 6 :

Expand (2 + x)⁶

(2 + x)⁶

Solution :

(a + b)⁶ = a⁶ + 6a⁵b + 15a⁴b² + 20a³b³ + 15a²b⁴ + 6ab⁵ + b⁶

a = 2 and b = x

Substitute 2 for a and x for b.

(2 + x)⁶ = (2)⁶ + 6(2)⁵(x) + 15(2)⁴(x)² + 20(2)³(x)³ + 15(2)²(x)⁴ + 6(2)(x)⁵ + x⁶

(2 + x)⁶ = 64 + 192x + 240x² + 160x³ + 60x⁴ + 12x⁵ + x⁶

Problem 7 :

Use the expansion of a to find the value of (2.01)⁶.

Solution :

a = 2.01 and b = 0

Substitute 2.01 for a and 0 for b.

(2.01 + 0)⁶ = (2.01)⁶ + 6(2.01)⁵(0) + 15(2.01)⁴(0)² + 20(2.01)³(0)³ + 15(2.01)²(0)⁴ + 6(2.01)(0)⁵ + (0)⁶

(2.01 + 0)⁶ = 65.944

So, the value of (2.01)⁶ is

65.944

Problem 8 :

Expand and simplify (2x + 3) (x + 1)⁴.

Solution :

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

= (2x + 3) (x + 1)⁴

= (2x + 3) (x⁴ + 4x³ + 6x² + 4x + 1)

= 2x(x⁴ + 4x³ + 6x² + 4x + 1) + 3(x⁴ + 4x³ + 6x² + 4x + 1)

= 2x⁵ + 8x⁴ + 12x³ + 8x² + 2x + 3x⁴ + 12x³ + 18x² + 12x + 3

= 2x⁵ + 11x⁴ + 24x³ + 26x² + 14x + 3

Problem 9 :

Find the coefficient of:

a³b² in the expansion of (3a + b)⁵

Solution :

Using pascal's triangle,

(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

(3a + b)⁵ = (3a)⁵ + 5(3a)⁴b + 10(3a)³b² + 10(3a)²b³ + 5(3a)b⁴ + b⁵

(3a + b)⁵ = 243a⁵ + 135a⁴b + 270a³b² + 90a²b³ + 15ab⁴ + b⁵

So, coefficient of a³b² is 270.

Problem 10 :

a³b³ in the expansion of (2a + 3b)⁶.

Solution :

(a + b)⁶ = a⁶ + 6a⁵b + 15a⁴b² + 20a³b³ + 15a²b⁴ + 6ab⁵ + b⁶

(2a + 3b)⁶ = (2a)⁶ + 6(2a)⁵(3b) + 15(2a)⁴(3b)² + 20(2a)³(3b)³ + 15(2a)²(3b)⁴ + 6(2a)(3b)⁵ + (3b)⁶

(2a + 3b)⁶ = 64a⁶ + 576a⁵b + 2160a⁴b² + 4320a³b³ + 4860a²b⁴ + 2916ab⁵ + 729b⁶

So, coefficient of a³b³ is 4320.