USING FINITE DIFFERENCES TO FIND THE DEGREE OF POLYNOMIALS

Use finite differences to determine the degree of the polynomial that best describes the data.

Problem 1 :

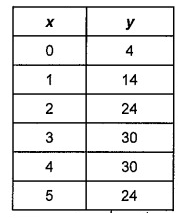
Solution:

Since fourth difference are same, it is polynomial of degree 4.

Problem 2 :

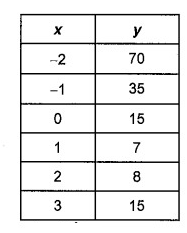
Solution:

Since third difference are same, it is cubic polynomial. The degree of the polynomial is 3.

Problem 3 :

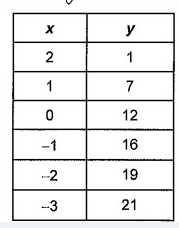
Solution:

Since second difference are same, it is a quadratic polynomial. The degree of the polynomial is 2.

Problem 4 :

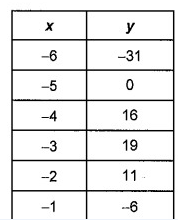
Solution:

Since third difference are same, it is cubic polynomial. The degree of the polynomial is 3.

Curve Fitting with Polynomial Models

Carla has been making a "wild scape" in her backyard. The table shows the number of birds visiting her feeder at the same hour

on the first day of each month since she began her project. Use a polynomial model to make a reasonable estimate of the number of birds there might be in July.

Problem 5 :

Use finite difference to determine the degree of the polynomial that best fits the data.

a. First differences ______

b. Second differences _____

c. Third differences _____

d. Fourth differences _____

e. Which degree polynomial best describes the data?

Solution:

Since third difference are same, it is cubic polynomial. The degree of the polynomial is 3.

Problem 6 :

Consider this data:

a. Calculate finite differences to find the degree of the polynomial function that models these data.

b. What is the minimum number of data points required to determine the degree of this polynomial function? Why?

c. Find the polynomial function that models these data and use it to find s when n is 12.

Solution:

a.

Since second difference are same, it is a quadratic polynomial. The degree of the polynomial is 2.

b.

y = ax² + bx + c

Put x = 1 and y = 1

1 = a(1)² + b(1) + c

1 = a + b + c ---> (1)

Put x = 2 and y = 3

3 = a(2)² + b(2) + c

3 = 4a + 2b + c ---> (2)

Put x = 3 and y = 6

6 = a(3)² + b(3) + c

6 = 9a + 3b + c ---> (3)

Add (1) & (2),

-3a - b = -2 ---> (4)

Add (1) & (4),

-2a + c = 1 ---> (5)

(2) × 3 ==> 12a + 6b + 3c = 9

(3) × 2 ==> 18a + 6b + 2c = 12

                    _______________

                      -6a + c = -3 ---> (6)

Add (5) & (6),

4a = 4

a = 1

By applying a = 1 in (5)

-2(1) + c = 1

c = 3

By applying a = 1 and c = 3 in (1)

1 + b + 3 = 1

4 + b = 1

b = -3

c. The quadratic polynomial,

s = 1n² - 3n + 3

When n = 12, s = ?

s = 1(12)² - 3(12) + 3

s = 144 - 36 + 3

s = 111