USING DISCRIMINANT TO FIND NUMBER OF SOLUTIONS

Role of discriminant to find number of solutions :

Without solving the equation completely, how we are finding the number of solutions for the quadratic function and how it would be.

The quadratic function which is in the form ax² + bx + c = 0 will have two solutions.

if b2 - 4ac > 0 There is two distinct solutions
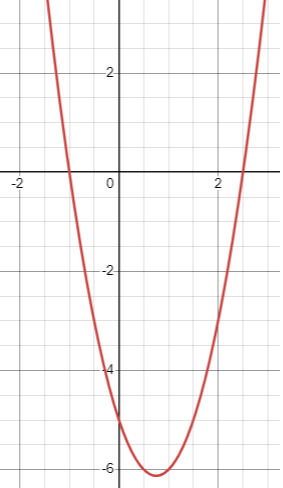if b2 - 4ac = 0 There is one solution
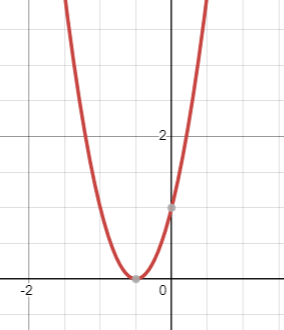if b2 - 4ac < 0 There is no solution

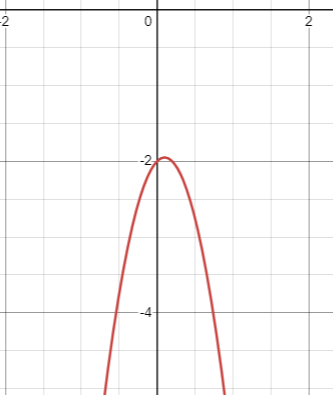The other words of solutions are, x-intercepts, zeroes, roots. To find solutions of quadratic equation, we have different methods.

Find the value of the discriminant to determine the number of zeros of each quadratic function.

Problem 1 :

f(x) = 2x² - 3x - 5

Solution :

Comparing the given quadratic function with

f(x) = ax² + bx + c

Here a = 2, b = -3 and c = -5

b² - 4ac = (-3)² - 4(2)(-5)

= 9 + 40

= 49

b² - 4ac > 0

Since the value of discriminant is greater than 0, the quadratic function will have two distinct solution.

Problem 2 :

f(x) = 4x² + 4x + 1

Solution :

Comparing the given quadratic function with

f(x) = ax² + bx + c

Here a = 4, b = 4 and c = 1

b² - 4ac = 4² - 4(4)(1)

= 16 - 16

= 0

b² - 4ac = 0

Since the value of discriminant is equal to 0, the quadratic function will have one solution.

Problem 3 :

f(x) = -5x² + x - 2

Solution :

Comparing the given quadratic function with

f(x) = ax² + bx + c

Here a = -5, b = 1 and c = -2

b² - 4ac = 1² - 4(-5)(-2)

= 1 - 40

= -39 < 0

Since the discriminant is less than 0, it has no solution.

Problem 4 :

Determine the value of k so that the quadratic function

f(x) = x² - kx + 3

has only one zero.

Solution :

Here a = 1, b = -k and c = 3

Since the given quadratic function has one zero, then

b² - 4ac = 0

(-k)² - 4(1)(3) = 0

k² - 12 = 0

k² = 12

k = √12

k = √(2 x 2 x 3)

k =  ± 2√3

Problem 5 :

For what values of k will the function 

f(x) = 3x² - 4x + k

have one x-intercept ?

Solution :

Here a = 3, b = -4 and c = k

Since the given quadratic function has one zero, then

b² - 4ac = 0

(-4)² - 4(3)(k) = 0

16 - 12k = 0

12 k = 16

k = 16/12

k = 4/3

Problem 6 :

For what values of k will the function 

f(x) = kx² - 4x + k

have no zero ?

Solution :

Here a = k, b = -4 and c = k

Since the given quadratic function has no zero, then

b² - 4ac < 0

(-4)² - 4(k)(k) < 0

16 - 4k² < 0

-4k² < -16

k² > 4

k > √4

k > ±2 

So, the solutions are k > 2 or k < -2.

Problem 7 :

The graph of the function

f(x) = x² - kx + (k + 8)

touches the x-axis at one point. what are the possible values of k ?

Solution :

Here a = 1, b = -k and c = k + 8

Since the given quadratic function has one zero, then

b² - 4ac = 0

(-k)² - 4(1)(k+8) = 0

k² - 4(k+8) = 0

k² - 4k - 32 = 0

Factoring the quadratic equation,

(k - 8) (k + 4) = 0

k = 8 and k = -4

So, the values of k are -4 and 8.

Problem 8 :

If f(x) = x² - 6x + 14 and g(x) = -x² - 20x - k

determine the value of k so that there is exactly one point of intersection between the two parabolas.

Solution :

f(x) = x² - 6x + 14 and g(x) = -x² - 20x - k

f(x) = g(x)

x² - 6x + 14 = -x² - 20x - k

x² + x²- 6x + 20x + 14 + k = 0

2x² + 14x + 14 + k = 0

Since there is one point of intersection,

b² - 4ac = 0

a = 2, b = 14 and c = 14 + k

14² - 4(2)(14+k) = 0

196 - 8(14 + k) = 0

196 - 112 - 8k = 0

84 - 8k = 0

8k = 84

k = 84/8

k = 21/2

So, the value of k is 10/2.