USE TRANSFORMATIONS TO GRAPH THE FUCTION FROM GIVEN GRAPH
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Considering the given function in the form
y = a (x - h) + k
Based on the signs, we decide what transformation can be made.
- If h > 0, then move the graph horizontally h units right.
- If h < 0, then Move the graph horizontally h units left.
- If k > 0, then move the graph k units up.
- If k < 0, then move the graph k units down.
- If a > 1, vertical stretch of a units.
- If 0 < a < 1, vertical shrink of a units.
Reflection :
- If f(x) = f(-x), then reflection across y-axis.
- If f(x) = -f(x), then reflection across x-axis.
Horizontal stretch or shrink :
If f(x) = f(ax),
then horizontal shrink of a units.
If f(x) = f(ax)
- a > 0 then horizontal shrink of a units.
- 0 < a < 1, horizontal stretch of of a units.
|
|
|
The graph of y = f(x) is given below. Sketch the graph of each of the following functions.
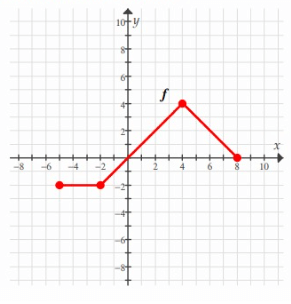
Problem 1 :
y = f(x + 2)
Solution :
y = f(x + 2)
y = f(x - (-2))
Here h = -2
Move the graph horizontally 2 units left.
|
A(-5, -2) B(-2, -2) C(0, 0) D(4, 4) E(8, 0) |
A'(-5-2, -2) ==> A'(-7, -2) B'(-2-2, -2) ==> B'(-4, -2) C'(0-2, 0) ==> C'(-2, 0) D'(4-2, 4) ==> D'(2, 4) E'(8-2, 0) ==> E'(6, 0) |
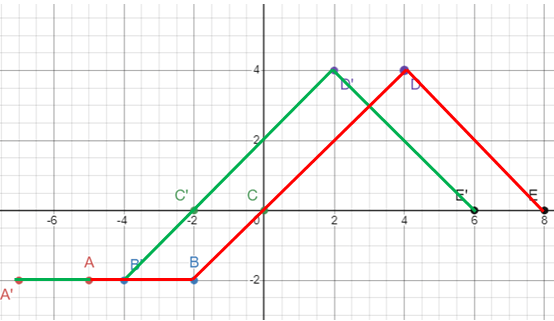
Problem 2 :
y = f(x) - 3
Solution :
y = f(x) - 3
Comparing with y = a f(x-h) + k
Here k = -3
Move the graph vertically 3 units down.
|
A(-5, -2) B(-2, -2) C(0, 0) D(4, 4) E(8, 0) |
A'(-5, -2-3) ==> A'(-5, -5) B'(-2, -2-3) ==> B'(-2, -5) C'(0, 0-3) ==> C'(0, -3) D'(4, 4-3) ==> D'(4, 1) E'(8, 0-3) ==> E'(8, -3) |
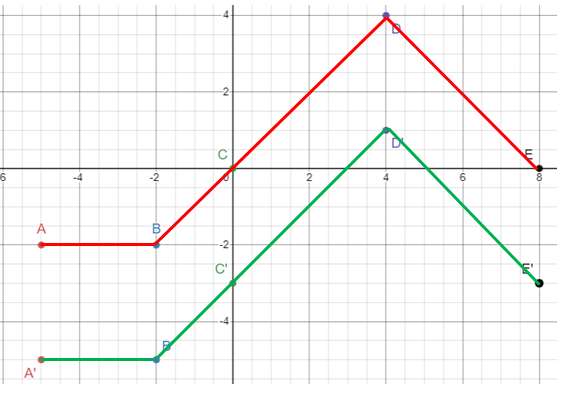
Problem 3 :
y = f(x - 2) - 1
Solution :
y = f(x - 2) - 1
Comparing with y = a f(x-h) + k
Here h = 2 and k = -1
Move the graph horizontally 2 units right and 1 unit down.
|
A(-5, -2) B(-2, -2) C(0, 0) D(4, 4) E(8, 0) |
A'(-5+2, -2-1) ==> A'(-3, -3) B'(-2+2, -2-1) ==> B'(0, -3) C'(0+2, 0-1) ==> C'(2, -1) D'(4+2, 4-1) ==> D'(6, 3) E'(8+2, 0-1) ==> E'(10, -1) |
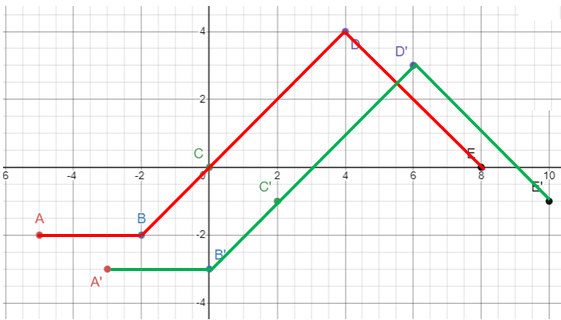
Problem 4 :
y = f(-x)
Solution :
y = f(-x)
Here x is changed as -x. So, reflection across y axis.
|
A(-5, -2) B(-2, -2) C(0, 0) D(4, 4) E(8, 0) |
A(-(-5), -2) ==> A'(5, -2) B(-(-2), -2) ==> B'(2, -2) C(0, 0) ==> C'(0, 0) D(-4, 4) ==> D'(-4, 4) E(-8, 0) ==> E'(-8, 0) |
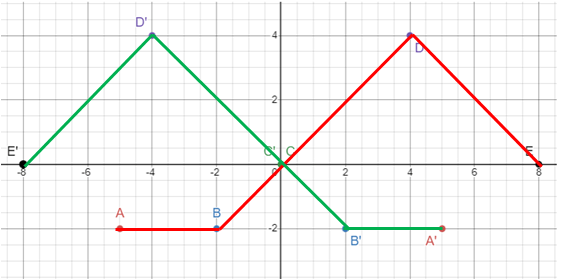
Problem 5 :
y = -f(x)
Solution :
y = -f(x)
Here y is changed as -y. So, reflection across x axis.
|
A(-5, -2) B(-2, -2) C(0, 0) D(4, 4) E(8, 0) |
A(-5, -(-2)) ==> A'(-5, 2) B(-2, -(-2)) ==> B'(-2, 2) C(0, 0) ==> C'(0, 0) D(4, -4) ==> D'(4, -4) E(8, 0) ==> E'(8, 0) |
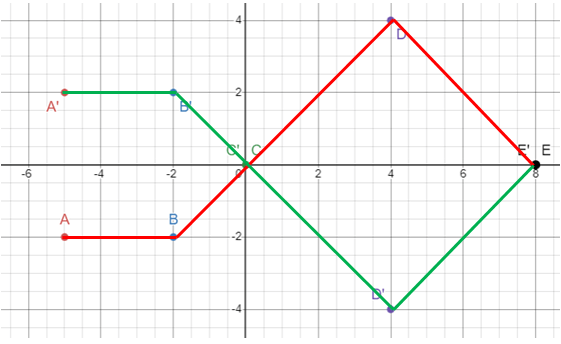
Problem 6 :
y = 2f(x)
Solution :
y = 2f(x)
Vertical stretch of 2 units.
|
A(-5, -2) B(-2, -2) C(0, 0) D(4, 4) E(8, 0) |
A(-5, 2(-2)) ==> A'(-5, -4) B(-2, 2(-2)) ==> B'(-2, -4) C(0, 2(0)) ==> C'(0, 0) D(4, 2(4)) ==> D'(4, 8) E(8, 2(0)) ==> E'(8, 0) |
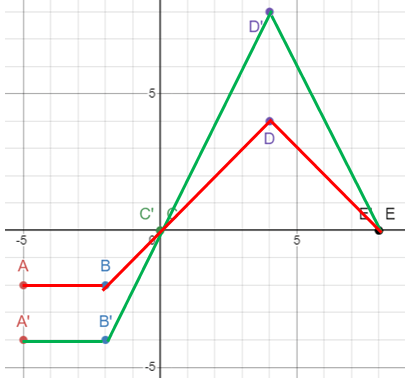
Problem 7 :
y = (1/2)f(x)
Solution :
y = (1/2)f(x)
Vertical shrink of 1/2 units.
|
A(-5, -2) B(-2, -2) C(0, 0) D(4, 4) E(8, 0) |
A(-5, -2/2) ==> A'(-5, -1) B(-2, -2/2) ==> B'(-2, -1) C(0, 0/2) ==> C'(0, 0) D(4, 4/2) ==> D'(4, 2) E(8, 0/2) ==> E'(8, 0) |
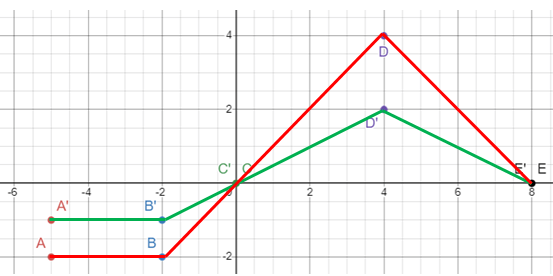
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling