USE SYNTHETIC SUBSTITUTION TO EVALUATE FOR THE GIVEN VALUE

Use synthetic division to evaluate the function for the indicated value of x.

Problem 1 :

f(x) = -x² - 8x + 30; x = -1

Solution :

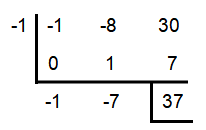
From the synthetic division above, we have

f(-1) = 37

Problem 2 :

f(x) = 3x² + 2x – 20; x = 3

Solution :

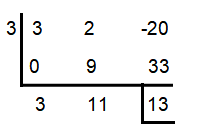
From the synthetic division above, we have

f(3) = 13

Problem 3 :

f(x) = x³ - 2x² + 4x + 3; x = 2

Solution :

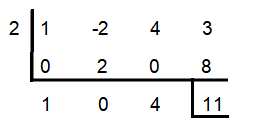
From the synthetic division above, we have

f(2) = 11

Problem 4 :

f(x) = x³ + x² - 3x + 9; x = -4

Solution :

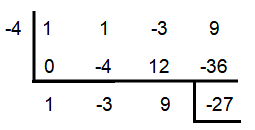
From the synthetic division above, we have

f(-4) = -27

Problem 5 :

f(x) = x³ - 6x + 1; x = 6

Solution :

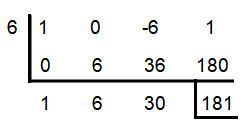
From the synthetic division above, we have

f(6) = 181

Problem 6 :

f(x) = x³ - 9x – 7; x = 10

Solution :

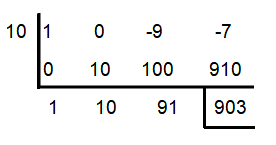
From the synthetic division above, we have

f(10) = 903

Problem 7 :

f(x) = x⁴ + 6x² - 7x + 1; x = 3

Solution :

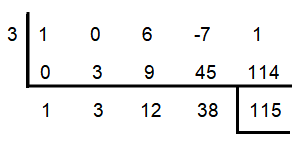
From the synthetic division above, we have

f(3) = 115

Problem 8 :

f(x) = -x⁴ - x³ - 2; x = 5

Solution :

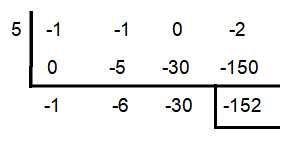
From the synthetic division above, we have

f(5) = -152

Problem 9 :

The profit P (in millions of dollars) for a DVD manufacturer can be modeled by

P = −6x³ + 72x

where x is the number (in millions) of DVDs produced. Use synthetic division to show that the company yields a profit of $96 million when 2 million DVDs are produced. Is there an easier method? Explain.

Solution :

P = −6x³ + 72x

When Number of DVD's produced = 2 million, then profit = 96 million. To prove this, we use the method of synthetic division.

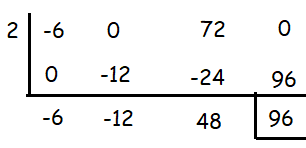
Yes, there is a easier way. Applying x = 2 in the original function, we will get the remainder.

Let P(x) = −6x³ + 72x

When x = 2

P(x) = −6(2)³ + 72(2)

= -6(8) + 144

= -48 + 144

= 96 million

Problem 10 :

You use synthetic division to divide f(x) by (x−a) and find that the remainder equals 15. Your friend concludes that f(15) = a. Is your friend correct? Explain your reasoning.

Solution :

Given that, while dividing the given polynomial f(x) by x - a, we get the remainder 15. Which means applying x = a, we get the remainder 15. Accordingly this understanding f(a) = 15

But your friend concludes that f(15) = a.  Then your friend's argument is incorrect.

Problem 11 :

The graph represents the polynomial function f(x) = x³ + 3x² − x − 3.

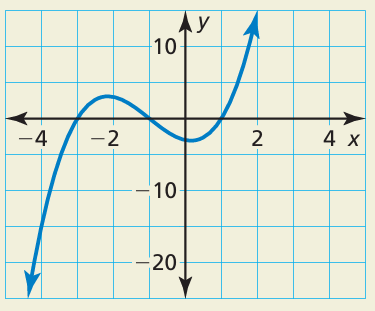
a. The expression f(x) ÷ (x − k) has a remainder of −15. What is the value of k?

b. Use the graph to compare the remainders of (x³ + 3x² − x − 3) ÷ (x + 3) and (x³ + 3x² − x − 3) ÷ (x + 1)

Solution :

a) Since the remainder is -15 which dividing the polynomial by the linear factor. By observing the curve, we know that one of the point is (-4, -15). When x = -4, the value of f(-4) is -15. From this, we understand that f(x) ÷ (x + 4), the remainder is -15. So, the value of k is -4.

b)

x + 3 = 0

x = -3

By observing the curve, it passes through the point (-3, 0). So, the remainder is 0 while dividing the polynomial by x + 3.

x + 1 = 0

x = -1

By observing the curve, it passes through the point (-1, 0). So, the remainder is 0 while dividing the polynomial by x + 1.

Problem 12 :

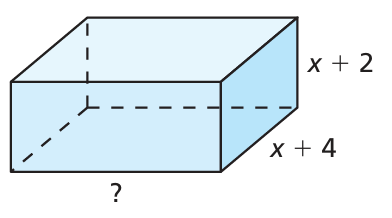
The volume V of the rectangular prism is given by V = 2x³ + 17x² + 46x + 40. Find an expression for the missing dimension.

Solution :

V = 2x³ + 17x² + 46x + 40

Volume of rectangular prism = length ⋅ width ⋅ height

Length = ?, width = x + 4 and height = x + 2

length ⋅ (x + 4) ⋅ (x + 2) = 2x³ + 17x² + 46x + 40

Length = (2x³ + 17x² + 46x + 40) / (x + 4)(x + 2)

x + 4 = 0 and x + 2 = 0

x = -4 and x = -2

Using synthetic division, let us divide the polynomial by x + 2.

2x² + 13x + 20

Now let us divide the polynomial by x + 4.

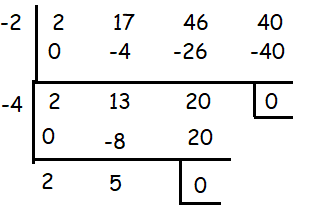
We get the quotient, which is 2x + 5.

So, the missing length of the rectangular prism is 2x + 5.

Problem 13 :

What is the value of k such that

f(x) = (x³ + kx² - 9x - 36)/(x + 4)

has a remainder of zero? Use the easier way.

Solution :

While dividing the polynomial by x + 4, we get the remainder 0. To do the problem in easiest way, we may apply x = -4 in the given polynomial.

f(x) = (x³ + kx² - 9x - 36)

x + 4 = 0

x = -4

f(-4) = (-4)³ + k(-4)² - 9(-4) - 36

0 = -64 + 16k + 36 - 36

0 = -64 + 16k

16k = 64

k = 64/16

k = 4

So, the value of k is 4.