USE DOUBLE ANGLE IDENTITIES TO FIND EXACT VALUE

Here we see the list of double angle formulae.

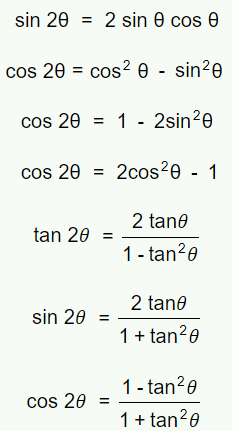
Problem 1 :

Given that sin A = 3/5 and cos A = -4/5, find 

i) sin 2A    ii)  cos 2A

Solution :

i) sin 2A 

To evaluate sin 2A, we can use double angle formula.

sin 2A = 2 sin A cos A

sin 2A = 2(3/5) (-4/5)

= -24/25

ii)  cos 2A :

cos 2A = cos² A - sin² A.

= (cos A)² - (sin A)²

= (-4/5)² - (3/5)²

= 16/25 - 9/25

= (16 - 9)/25

= 7/25

Problem 2 :

Given that sin A = -5/13 and cos A = 12/13, find tan 2A.

Solution :

Problem 3 :

If A is acute angle and cos 2A = 3/4, find the values of 

i) cos A 

ii) sin A

Solution :

cos 2A = 3/4

cos 2A = 2 cos²A - 1

3/4 = 2 cos²A - 1

2 cos²A = (3/4) + 1

2 cos²A = (7/4)

cos²A = (7/8)

ii) sin A

cos 2A = 1 - 2 sin²A

3/4 = 1 - 2 sin²A

2 sin²A = 1 - (3/4)

2 sin²A = 1/4

sin²A = 1/8

sin A = 1/2√2

Problem 4 :

If sin A = 4/5 and cos A = 3/5, find the values of 

i) sin 2A

ii) cos 2A

Solution :

i) sin 2A = 2 sin A cos A

= 2 (4/5) (3/5)

sin 2A = 24/25

ii) cos 2A = cos² A - sin² A

= (cos A)² - (sin A)²

= (4/5)² - (3/5)²

= (16/25) - (9/25)

= 7/25

Problem 5 :

If sin A = -2/3 where π < A < 3π/2, find the value of cos A and hence the value of sin 2A.

Solution :

From the given information, it is clear the angle lies on 3rd quadrant. In 3rd quadrant, for tangent and its reciprocal only cotangent will have positive sign. 

Problem 6 :

If cos A = 2/5, where 3π/2 < A < 2π, find the value of sin A hence find the value of sin 2A.

Solution :

From the given information, it is clear the angle lies on 4th quadrant. In 4th quadrant, for cosine and its reciprocal only secant will have positive sign. 

Problem 7 :

If A is acute cos 2A = -7/9, find without calculator 

i) cos A

ii) sin A

Solution :

i) cos A

cos 2A = 2 cos²A - 1

(-7/9) = 2 cos²A - 1

(-7/9) + 1 = 2 cos²A

2 cos²A = 2/9

cos²A = 1/9

cos A = √(1/9)

cos A = 1/3

ii) sin A

cos 2A = 1 - 2 sin²A

(-7/9) = 1 - 2 sin²A

2 sin²A = 1 + (7/9)

2 sin²A = 16/9

sin²A = 8/9

sin A = √(8/9)

sin A = 2√2/3

Problem 8 :

Find the value of 

Solution :

Problem 9 :

Show that

(sin A + cos A)² = 1 + sin 2A

Solution :

L.H.S

= (sin A + cos A)²

Finding expansion using algebraic identity, we get

= sin² A + cos² A + 2sin A cos A

= 1 + sin 2A

Problem 10 :

Show that

cos⁴A - sin⁴A = cos 2A

Solution :

L.H.S

= cos⁴A - sin⁴A

= (cos²A)² - (sin²A)²

Using the algebraic identity, a² - b² = (a + b)(a - b)

= (cos²A + sin²A)(cos²A - sin²A)

= 1(cos 2A)

= cos 2A